
如圖,已知四棱錐S―ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,且O到AB、AD的距離分別為2和1.
(I)求證![]() 是定值;
是定值;
(II)已知P是SC的中點,且SO=3,問在棱SA上是否存在一點Q,使得異面直線OP與BQ所成的角為90°?若存在,請給出證明,并求出AQ的長;若不存在,請說明理由.

解:法一:(I)以O為坐標原點,以OS所在直線為Oz軸,過O且平行于AD的直線為Ox軸.過O且平行于AB的直線為Oy軸,建立如圖所示空間直角坐標系
設S(0,0,z)(z>0,z∈R)
則![]()
![]()
即![]() 為定值
為定值
(II)由(I)建立的空間直角坐標系可知
A(2,-1,0),B(2,3,0)C(-2,3,0),S(0,0,3)
P(-1,![]() )
)
設點Q(x,y,z),則存在λ使![]()

法二:(I)證明:在△SDC內,作SE⊥CD交CD于E,連結OE
∵SO⊥平面ABCD ∴SO⊥CD
∴CD⊥平面SOE ∴SO⊥OE
∴OE//AD ∴DE=1
從而CE=3
![]()
即![]() 為定值
為定值
(II)利用其它方法求解同樣可得分


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
 如圖,已知四棱錐S-ABCD的底面ABCD是邊長為1的正方形,SA⊥平面ABCD,SA=2,E是側棱SC上的一點.
如圖,已知四棱錐S-ABCD的底面ABCD是邊長為1的正方形,SA⊥平面ABCD,SA=2,E是側棱SC上的一點.查看答案和解析>>
科目:高中數學 來源: 題型:
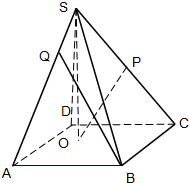 如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,SO的長為3,O到AB,AD的距離分別為2和1,P是SC的中點.
如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,SO的長為3,O到AB,AD的距離分別為2和1,P是SC的中點.| AQ |
| 3 |
| 4 |
| AS |
查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
 (2008•湖北模擬)如圖,已知四棱錐S-ABCD中,△SAD是邊長為a的正三角形,平面SAD⊥平面ABCD,四邊形ABCD為菱形,∠DAB=60°,P為AD的中點,Q為SB的中點.
(2008•湖北模擬)如圖,已知四棱錐S-ABCD中,△SAD是邊長為a的正三角形,平面SAD⊥平面ABCD,四邊形ABCD為菱形,∠DAB=60°,P為AD的中點,Q為SB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2010•江西模擬)(如圖)已知四棱錐S-ABCD的底面ABCD是菱形,將面SAB,SAD,ABCD 展開成平面后的圖形恰好為一正三角形S'SC.
(2010•江西模擬)(如圖)已知四棱錐S-ABCD的底面ABCD是菱形,將面SAB,SAD,ABCD 展開成平面后的圖形恰好為一正三角形S'SC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com