
【題目】已知四面體有五條棱長為3,且外接球半徑為2.動點P在四面體的內部或表面,P到四個面的距離之和記為s.已知動點P在![]() ,
,![]() 兩處時,s分別取得最小值和最大值,則線段
兩處時,s分別取得最小值和最大值,則線段![]() 長度的最小值為______.
長度的最小值為______.
【答案】![]()
【解析】
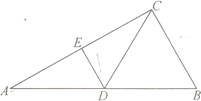
設四面體為![]() ,其中
,其中![]() ,取
,取![]() 的中點分別為
的中點分別為![]() ,求出
,求出![]() 的長,將點
的長,將點![]() 到四個面的距離之和記為s,轉化為到其中兩個面的距離,利用等體積的方法分析出距離之和的最值,從而得到線段
到四個面的距離之和記為s,轉化為到其中兩個面的距離,利用等體積的方法分析出距離之和的最值,從而得到線段![]() 長度的最小值為
長度的最小值為![]() ,
,![]() 上兩點間的距離的最小值,得到答案.
上兩點間的距離的最小值,得到答案.
四面體為![]() ,其中
,其中![]() ,設
,設![]() .
.
取![]() 的中點分別為
的中點分別為![]() ,連接
,連接![]() ,如圖.
,如圖.
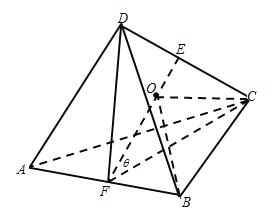
在等腰三角形![]() 中,有
中,有![]() .
.
所以![]() 平面
平面![]() ,又
,又![]() 為
為![]() 的中點.
的中點.
則四面體![]() 的外接球的球心
的外接球的球心![]() 一定在平面
一定在平面![]() 上.
上.
同理可得四面體![]() 的外接球的球心
的外接球的球心![]() 一定在平面
一定在平面![]() 上.
上.
所以四面體![]() 的外接球的球心
的外接球的球心![]() 一定在
一定在![]() 上.
上.
連接![]() ,設
,設![]() .
.
在直角三角形![]() 中,
中,![]() .
.
在三角形![]() 中,
中,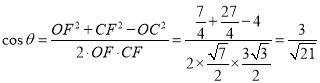 .
.
在直角三角形![]() 中,
中,![]() .
.
所以![]() 長為定值,
長為定值,![]() 的長為定值.
的長為定值.
根據條件有![]() ,設為
,設為![]() ,
, ![]() ,設為
,設為![]()
設點![]() 到四個面
到四個面![]() ,
,![]() ,
,![]() ,
,![]() 的距離分別為
的距離分別為![]() .
.
設四面體![]() 的體積為
的體積為![]() (為定值)
(為定值)
由等體積法有:![]()
所以![]()
所以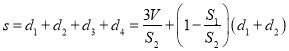
當點![]() 在
在![]() 上時,
上時,![]() 最小.
最小.
當點![]() 遠離
遠離![]() 時,
時,![]() 的值增大,
的值增大,
由等體積法可得當點![]() 在
在![]() 上時,
上時,![]() 的值相等,且此時
的值相等,且此時![]() 的值最大.
的值最大.
所以當點![]() 在
在![]() 或
或![]() 上時,
上時,![]() 取得最值.
取得最值.
故線段![]() 長度的最小值為
長度的最小值為![]() ,
,![]() 上兩點間的距離的最小值.
上兩點間的距離的最小值.
由上可知,![]() .
.
所以![]() ,
,![]() 上兩點間的距離的最小值為
上兩點間的距離的最小值為![]() .
.
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某地實行垃圾分類后,政府決定為![]() 三個小區建造一座垃圾處理站M,集中處理三個小區的濕垃圾.已知
三個小區建造一座垃圾處理站M,集中處理三個小區的濕垃圾.已知![]() 在
在![]() 的正西方向,
的正西方向,![]() 在
在![]() 的北偏東
的北偏東![]() 方向,
方向,![]() 在
在![]() 的北偏西
的北偏西![]() 方向,且在
方向,且在![]() 的北偏西
的北偏西![]() 方向,小區
方向,小區![]() 與
與![]() 相距
相距![]() 與
與![]() 相距
相距![]() .
.
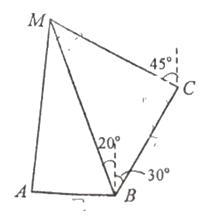
(1)求垃圾處理站![]() 與小區
與小區![]() 之間的距離;
之間的距離;
(2)假設有大、小兩種運輸車,車在往返各小區、處理站之間都是直線行駛,一輛大車的行車費用為每公里![]() 元,一輛小車的行車費用為每公里
元,一輛小車的行車費用為每公里![]() 元(其中
元(其中![]() 為滿足
為滿足![]() 是
是![]() 內的正整數) .現有兩種運輸濕垃圾的方案:
內的正整數) .現有兩種運輸濕垃圾的方案:
方案1:只用一輛大車運輸,從![]() 出發,依次經
出發,依次經![]() 再由
再由![]() 返回到
返回到![]() ;
;
方案2:先用兩輛小車分別從![]() 運送到
運送到![]() ,然后并各自返回到
,然后并各自返回到![]() ,一輛大車從
,一輛大車從![]() 直接到
直接到![]() 再返回到
再返回到![]() .試比較哪種方案更合算?請說明理由. 結果精確到小數點后兩位
.試比較哪種方案更合算?請說明理由. 結果精確到小數點后兩位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,將![]() 方格紙中每個小方格染三種顏色之一,使得每種顏色的小方格的個數相等.若相鄰兩個小方格的顏色不同,稱他們的公共邊為“分割邊”,則分割邊條數的最小值為( )
方格紙中每個小方格染三種顏色之一,使得每種顏色的小方格的個數相等.若相鄰兩個小方格的顏色不同,稱他們的公共邊為“分割邊”,則分割邊條數的最小值為( )

A.33B.56C.64D.78
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分形幾何是美籍法國數學家芒德勃羅在20世紀70年代創立的一門數學新分支,其中的“謝爾賓斯基”圖形的作法是:先作一個正三角形,挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的每個小正三角形中又挖去一個“中心三角形”.按上述方法無限連續地作下去直到無窮,最終所得的極限圖形稱為“謝爾賓斯基”圖形(如圖所示),按上述操作7次后,“謝爾賓斯基”圖形中的小正三角形的個數為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() ,如圖1.以
,如圖1.以![]() 為折痕將
為折痕將![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,如圖2.
的位置,如圖2.

如圖1 如圖2
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數據![]() 是鄭州市普通職工
是鄭州市普通職工![]() 個人的年收入,若這
個人的年收入,若這![]() 個數據的中位數為
個數據的中位數為![]() ,平均數為
,平均數為![]() ,方差為
,方差為![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,則這
,則這![]() 個數據中,下列說法正確的是( )
個數據中,下列說法正確的是( )
A.年收入平均數大大增大,中位數一定變大,方差可能不變
B.年收入平均數大大增大,中位數可能不變,方差變大
C.年收入平均數大大增大,中位數可能不變,方差也不變
D.年收入平均數可能不變,中位數可能不變,方差可能不變
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com