

 、
、 坐標,利用垂直向量數(shù)量積為零的方法建立方程組,解出
坐標,利用垂直向量數(shù)量積為零的方法建立方程組,解出 是平面AB'C的一個法向量;同樣的方法算出
是平面AB'C的一個法向量;同樣的方法算出 是平面ABP的一個法向量,利用空間向量的夾角公式算出
是平面ABP的一個法向量,利用空間向量的夾角公式算出 =
= ,結合圖形加以觀察即可得到二面角B-AP-C的余弦值.
,結合圖形加以觀察即可得到二面角B-AP-C的余弦值. 解:(Ⅰ)根據(jù)題意,可得△ABC為直角三角形,
解:(Ⅰ)根據(jù)題意,可得△ABC為直角三角形, =2,-----(1分)
=2,-----(1分) r=1,-----------------------------(2分)
r=1,-----------------------------(2分) ;-----------(5分)
;-----------(5分) ,
, ,
, ,
, ,取x=1,得y=0,z=-4,所以
,取x=1,得y=0,z=-4,所以 --------------------(7分)
--------------------(7分) ,由
,由 算出
算出 ,可得
,可得 ;-------------(10分)
;-------------(10分) ,設平面ABP的法向量
,設平面ABP的法向量 ,
, ,取y'=1,可得
,取y'=1,可得 ;-------------------------------(12分)
;-------------------------------(12分) =
= =
= ,
, 互為補角
互為補角 .------------------------------------(14分)
.------------------------------------(14分)

科目:高中數(shù)學 來源: 題型:
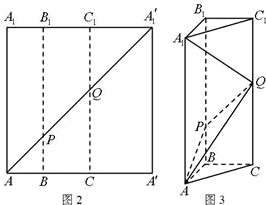 如圖2所示,在邊長為12的正方形AA'A'1A1中,點B,C在線段AA'上,且AB=3,BC=4,作BB1∥AA1,分別交A1A'1、AA'1于點B1、P,作CC1∥AA1,分別交A1A'1、AA'1于點C1、Q,將該正方形沿BB1、CC1折疊,使得A'A1′與AA1重合,構成如圖3所示的三棱柱ABC-A1B1C1.
如圖2所示,在邊長為12的正方形AA'A'1A1中,點B,C在線段AA'上,且AB=3,BC=4,作BB1∥AA1,分別交A1A'1、AA'1于點B1、P,作CC1∥AA1,分別交A1A'1、AA'1于點C1、Q,將該正方形沿BB1、CC1折疊,使得A'A1′與AA1重合,構成如圖3所示的三棱柱ABC-A1B1C1.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
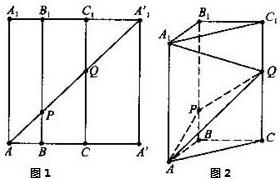 如圖1所示,在邊長為12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分別交BB1,CC1于點P、Q,將該正方形沿BB1、CC1折疊,使得A′A′1與AA1重合,構成如圖2所示的三棱柱ABC-A1B1C1,請在圖2中解決下列問題:
如圖1所示,在邊長為12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分別交BB1,CC1于點P、Q,將該正方形沿BB1、CC1折疊,使得A′A′1與AA1重合,構成如圖2所示的三棱柱ABC-A1B1C1,請在圖2中解決下列問題:查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
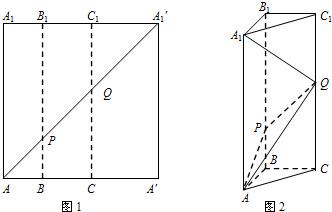 如圖1所示,在邊長為12的正方形AA′A1′A1中,點B,C在線段AA′上,且AB=3,BC=4,作BB1∥AA1,分別交A1A1′、AA1′于點B1、P,作CC1∥AA1,分別交A1A1′、AA1′于點C1、Q,將該正方形沿BB1、CC1折疊,使得A′A1′與AA1重合,構成如圖2所示的三棱柱ABC-A1B1C1.
如圖1所示,在邊長為12的正方形AA′A1′A1中,點B,C在線段AA′上,且AB=3,BC=4,作BB1∥AA1,分別交A1A1′、AA1′于點B1、P,作CC1∥AA1,分別交A1A1′、AA1′于點C1、Q,將該正方形沿BB1、CC1折疊,使得A′A1′與AA1重合,構成如圖2所示的三棱柱ABC-A1B1C1.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (Ⅰ)求直三棱柱ABC-A′B′C′的體積;
(Ⅰ)求直三棱柱ABC-A′B′C′的體積;查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com