【題目】已知函數
（
，且
）在
上單調遞增，且關于
的方程
恰有兩個不相等的實數解，則
的取值范圍是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由題意首先求得a的取值范圍，然后結合函數的解析式將原問題轉化為兩函數圖像存在兩個交點的問題，數形結合即可確定a的取值范圍.
由函數的解析式可知函數在區間
上單調遞增，
當
時，函數
單調遞減，由復合函數的單調性法則可知：
，
且函數在
處滿足：
，解得：
，故
，
方程
恰有兩個不相等的實數解，則函數
與函數
的圖像有且僅有兩個不同的交點，
繪制函數的圖像如圖中虛線所示，
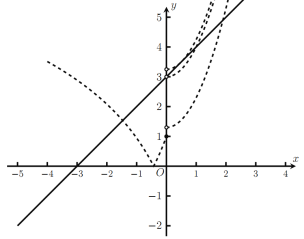
令
可得：
，
由可知
，
，
則直線與函數的圖像在區間
上存在唯一的交點，
原問題轉化為函數與二次函數
在區間上存在唯一的交點，
很明顯當
，即
時滿足題意，
當直線與二次函數相切時，設切點坐標為
，亦即
，
由函數的解析式可得：
，故：
，則
，
切點坐標為
，從而：
，即
.
據此可得：
的取值范圍是
.
故選：D.
科目：高中數學 來源： 題型：
【題目】點
、
、
分別是正方體
的棱
,
,
的中點,則下列命題中的真命題是__________（寫出所有真命題的序號）.
①以正方體的頂點為頂點的三棱錐的四個面中最多可以四個面都是直角三角形;
②點
在直線
上運動時,總有
;
③點
在直線上運動時,三棱錐
的體積是定值;
④若
是正方體的面
,（含邊界）內一動點,且點到點
和
的距離相等,則點的軌跡是一條線段.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】C反應蛋白（CRP）是機體受到微生物入侵或組織損傷等炎癥性刺激時細胞合成的急性相蛋白，醫學認為CRP值介于0-10mg/L為正常值.下面是某患者在治療期間連續5天的檢驗報告單中CRP值（單位：mg/L）與治療大數的統計數據：
治療天數x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
（1）若CRP值y與治療數x只有線性相關關系試用最小乘法求出y關于x的線性回歸方程，并估計該者至少需要治療多少天CRP值可以回到正常水平；
（2）為均衡城鄉保障待遇，統一保障范同和支付準，為多保人員提供公平的基本醫療保障.某市城鄉醫療保險實施辦法指出：門診報銷比例為50％；住院報銷比例，A類醫療機構80％，B類醫療機構60％.若張華參加了城鄉基本醫療保險，他因CRP偏高選擇在醫療機構治療，醫生為張華提供了三種治療方案：方案一：門診治療，預計每天診療費80元；方案二：住院治療，A類醫療機構，入院檢查需花費600元，預計每天診療費100元；方案三：住院治療，B類醫療機構，入院檢查需花費400元，預計每天診療費40元；若張華需要經過連續治療n天
，請你為張華選擇最經濟實惠的治療方案.
，
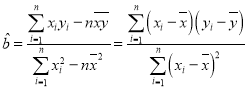查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】C反應蛋白（CRP）是機體受到微生物入侵或組織損傷等炎癥性刺激時肝細胞合成的急性相蛋白，醫學認為CRP值介于0-10mg/L為正常值下面是某患者在治療期間連續5天的檢驗報告單中CRP值（單位：mg/L）與治療天數的統計數據：
治療天數x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
（1）若CRP值y與治療天數x具有線性相關關系，試用最小二乘法求出y關于x的線性回歸方程，并估計該患者至少需要治療多少天CRP值可以到正常水平；
（2）為均衡城鄉保障待遇，統一保障范圍和支付標準，為參保人員提供公平的基本醫療保障.某市城鄉醫療保險實施辦法指出：門診報銷比例為50％：住院報銷比例，A類醫療機構80％，B類醫療機構60％.若張華參加了城鄉基本醫療保險，他因CRP偏高選擇在某醫療機構治療，醫生為張華提供了三種治療方案：
方案一：門診治療，預計每天診療費80元；
方案二：住院治療，A類醫療機構，入院檢查需花費600元，預計每天診療費100元；
方案三：住院治療，B類醫療機構，入院檢查需花費400元，預計每天診療費40元；
若張華需要經過連續治療n天，
，請你為張華選擇最經濟實惠的治療方案．
，
.
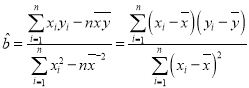查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列五個命題：
①“
”是“
為R上的增函數”的充分不必要條件；
②函數
有兩個零點；
③集合A={2，3}，B={1，2，3}，從A，B中各任意取一個數，則這兩數之和等于4的概率是
；
④動圓C即與定圓
相外切，又與y軸相切，則圓心C的軌跡方程是
⑤若對任意的正數x，不等式
恒成立，則實數
的取值范圍是
其中正確的命題序號是_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
是衡量空氣污染程度的一個指標，為了了解
市空氣質量情況，從
年每天的值的數據中隨機抽取
天的數據，其頻率分布直方圖如圖所示.將值劃分成區間
、
、
、
，分別稱為一級、二級、三級和四級，統計時用頻率估計概率 .
（1）根據年的數據估計該市在
年中空氣質量為一級的天數；
（2）如果市對環境進行治理，經治理后，每天值
近似滿足正態分布
，求經過治理后的值的均值下降率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】畫糖是一種以糖為材料在石板上進行造型的民間藝術，常見于公園與旅游景點.某師傅制作了一種新造型糖畫，為了進行合理定價先進性試銷售，其單價
（元）與銷量
（個）相關數據如下表：
（1）已知銷量與單價具有線性相關關系，求關于的線性相關方程；
（2）若該新造型糖畫每個的成本為
元，要使得進入售賣時利潤最大，請利用所求的線性相關關系確定單價應該定為多少元？（結果保留到整數）
參考公式：線性回歸方程
中斜率和截距最小二乘法估計計算公式：
.參考數據：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
