
【題目】已知函數![]() .
.
![]() 若函數
若函數![]() 在
在![]() 內有且只有一個零點,求此時函數
內有且只有一個零點,求此時函數![]() 的單調區間;
的單調區間;
![]() 當
當![]() 時,若函數
時,若函數![]() 在
在![]() 上的最大值和最小值的和為1,求實數a的值.
上的最大值和最小值的和為1,求實數a的值.
【答案】(1)見解析;(2)![]()
【解析】
![]() 求出函數的導數,得到極值點,當
求出函數的導數,得到極值點,當![]() 時,當
時,當![]() 時,判斷導函數的符號,得到函數的單調性,利用函數的極值結合函數的零點推出函數
時,判斷導函數的符號,得到函數的單調性,利用函數的極值結合函數的零點推出函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;![]() 當
當![]() 時,函數
時,函數![]() 有兩個極值點,推出
有兩個極值點,推出![]() ,
,![]() .
.![]() 若
若![]() ,由
,由![]() 可得
可得![]() 的值;
的值;![]() 若
若![]() ,由
,由![]() 可得
可得![]() ,不符合題意舍去,通過
,不符合題意舍去,通過![]() 若
若![]() ;
;![]() 若
若![]() ,轉化求解即得到實數
,轉化求解即得到實數![]() 的值.
的值.
![]() ,
,
![]() 由
由![]() ,得到
,得到![]() ,
,![]() ,
,
當![]() 時,
時,![]() 在區間
在區間![]() 上恒成立,
上恒成立,
即函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
又因為函數![]() 的圖象過點
的圖象過點![]() ,即
,即![]() ,
,
所以函數![]() 在
在![]() 內沒有零點,不合題意,
內沒有零點,不合題意,
當![]() 時,由
時,由![]() 得
得![]() ,即函數
,即函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
由![]() 得
得![]() ,即函數
,即函數![]() 在區間在
在區間在![]() 上單調遞減,
上單調遞減,
且過點![]() ,要使函數
,要使函數![]() 在
在![]() 內有且只有一個零點,則須
內有且只有一個零點,則須![]() ,
,
即![]() ,解得
,解得![]() ,
,
綜上可得函數![]() 在
在![]() 內有且只有一個零點時
內有且只有一個零點時![]() ,
,
此時函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,單調遞減區間為
,單調遞減區間為![]()
![]() 當
當![]() 時,函數
時,函數![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
此時函數![]() 有兩個極值點,極大值為
有兩個極值點,極大值為![]() ,極小值為
,極小值為![]() ,
,
且![]() ,
,![]() ,,
,,
![]() 若
若![]() ,即
,即![]() ,也即
,也即![]() 時,此時
時,此時![]() ,
,
又![]() ,
,![]()
由![]() 可得
可得![]() ,即
,即![]() ,符合題意
,符合題意
![]() 若
若![]() ,即
,即![]() ,也即
,也即![]() 時,
時,
此時![]() ,
,![]() ,
,
由![]() 可得
可得![]() ,即
,即![]() ,不符合題意舍去,
,不符合題意舍去,
又![]()
![]() ,
,
![]() 若
若![]() ,即
,即![]() ,也即
,也即![]() 時,此時
時,此時![]() ,
,
由![]() 可得
可得![]() ,即
,即![]() ,不符合題意舍去
,不符合題意舍去
![]() 若
若![]() ,即
,即![]() ,也即
,也即![]() 時,此時
時,此時![]() ,
,
由![]() 可得
可得![]() ,即
,即![]() ,不符合題意舍去,
,不符合題意舍去,
綜上所述可知所求實數a的值為![]()


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:
【題目】下列四個判斷正確的是______(寫出所有正確判斷的序號.)
①函數![]() 是奇函數,但不是偶函數;
是奇函數,但不是偶函數;
②函數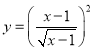 與函數
與函數![]() 表示同一個函數;
表示同一個函數;
③已知函數![]() 圖象的一條對稱軸為
圖象的一條對稱軸為![]() ,則
,則![]() 的值為
的值為![]() ;
;
④設函數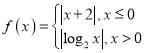 ,若關于
,若關于![]() 的方程
的方程![]() 有四個不同的解
有四個不同的解![]() ,且
,且![]() ,則
,則![]() 的值為
的值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,直線
,直線![]() :
:![]() ,圓
,圓![]() :
:![]() .
.
(1)求![]() 的取值范圍,并求出圓心坐標;
的取值范圍,并求出圓心坐標;
(2)若圓![]() 的半徑為1,過點
的半徑為1,過點![]() 作圓
作圓![]() 的切線,求切線的方程;
的切線,求切線的方程;
(3)有一動圓![]() 的半徑為1,圓心在
的半徑為1,圓心在![]() 上,若動圓
上,若動圓![]() 上存在點
上存在點![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為研究工人的日平均生產量是否與年齡有關,現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,再將兩組工人的日平均生產件數分為5組:![]()
![]()
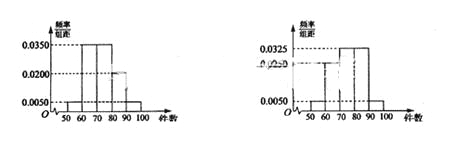
![]() 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.
(I)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的概率;
(II)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成列聯表,并判斷是否有90%的把握認為“生產能手與工人所在的年齡組有關”?
![]()
![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
25周歲以上組 25周歲以下組
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的各項均為正數,2a2﹣5a1=3,a3a7=9a42;
(1)求數列{an}的通項公式;
(2)設bn=anlog3an,求數列{bn}的前n項和Sn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com