
將一顆骰子拋擲兩次,所得向上點數分別為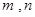 ,則函數
,則函數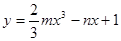 在
在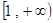 上為增函數的概率是 ( )
上為增函數的概率是 ( )
A.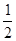 | B.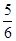 | C.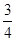 | D. |
B
解析試題分析:將一骰子向上拋擲兩次,所得點數分別為m和n的基本事件個數有36個.函數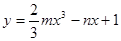 在[1,+∞)上為增函數包含的基本事件個數為30個,利用古典概型公式即可得到答案.解:函數
在[1,+∞)上為增函數包含的基本事件個數為30個,利用古典概型公式即可得到答案.解:函數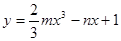 在[1,+∞)上為增函數,等價于導數y′=2mx2-n 在[1,+∞)上大于或等于0恒成立.而x2≥
在[1,+∞)上為增函數,等價于導數y′=2mx2-n 在[1,+∞)上大于或等于0恒成立.而x2≥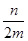 在[1,+∞)上恒成立即
在[1,+∞)上恒成立即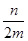 ≤1.∵將一骰子向上拋擲兩次,所得點數分別為m和n的基本事件個數為36個,而滿足
≤1.∵將一骰子向上拋擲兩次,所得點數分別為m和n的基本事件個數為36個,而滿足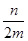 ≤1包含的(m,n)基本事件個數為30個,故函數
≤1包含的(m,n)基本事件個數為30個,故函數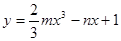 在[1,+∞)上為增函數的概率是
在[1,+∞)上為增函數的概率是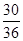 =
=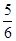 ,故答案為B.
,故答案為B.
考點:等可能事件的概率
點評:本題考查的是概率與函數的綜合問題,利用古典概型的特點分別求出基本事件的總數及所求事件包含的基本事件的個數,利用導數解決函數的恒成立問題,屬于中檔題


 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源: 題型:單選題
已知服從正態分布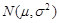 的隨機變量,在區間
的隨機變量,在區間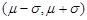 ,
,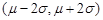 和
和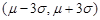 內取值的概率分別為
內取值的概率分別為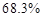 ,
,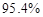 和
和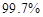 .某大型國有企業為
.某大型國有企業為 名員工定制工作服,設員工的身高(單位:
名員工定制工作服,設員工的身高(單位: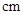 )服從正態分布
)服從正態分布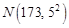 ,則適合身高在
,則適合身高在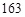 ~
~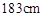 范圍內員工穿的服裝大約要定制( )
范圍內員工穿的服裝大約要定制( )
A.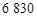 套 套 | B.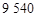 套 套 | C.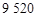 套 套 | D.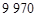 套 套 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
如圖;現有一迷失方向的小青蛙在3處,它每跳動一次可以等機會地進入相鄰的任意一格(如若它在5處,跳動一次,只能進入3處,若在3處,則跳動一次可以等機會進入l,2,4,5處),則它在第三次跳動后, 進入5處的概率是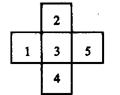
A. | B.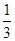 |
C.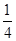 | D.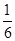 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
甲乙兩隊進行排球比賽,已知每一局比賽中甲隊獲勝的概率是 ,沒有平局.采用三局兩勝制比賽,即先勝兩局者獲勝且比賽結束,則甲隊獲勝的概率等于( )
,沒有平局.采用三局兩勝制比賽,即先勝兩局者獲勝且比賽結束,則甲隊獲勝的概率等于( )
A. | B. | C.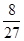 | D. |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com