
如圖,已知,在空間四邊形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若![]() ,求幾何體
,求幾何體![]() 的體積;
的體積;
(3)若![]() 為△
為△![]() 的重心,試在線段
的重心,試在線段![]() 上找一點
上找一點![]() ,使得
,使得![]() ∥平面
∥平面![]() .
.
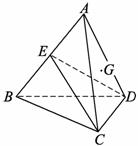
(1) 證明:∵BC=AC,E為AB的中點,∴AB⊥CE.
又∵AD=BD,E為AB的中點∴AB⊥DE. ∵![]()
∴AB⊥平面DCE∵AB![]() 平面ABC,∴平面CDE⊥平面ABC.
平面ABC,∴平面CDE⊥平面ABC.
(2)∵在△BDC中,DC=3,BC=5,BD=4,∴CD⊥BD,在△ADC中,DC=3,AD=BD=4,AC=BC=5,∴CD⊥AD,
∵![]() ∴CD⊥平面ABD.所以線段CD的長是三棱錐C-ABD的高。又在△ADB中,DE=
∴CD⊥平面ABD.所以線段CD的長是三棱錐C-ABD的高。又在△ADB中,DE=![]() ∴VC-ABD=
∴VC-ABD=![]() (3)在AB上取一點F,使AF=2FE,則可得GF∥平面CDE 取DC的中點H,連AH、EH∵G為△ADC的重心,∴G在AH上,且AG=2GH,連FG,則FG∥EH又∵FG
(3)在AB上取一點F,使AF=2FE,則可得GF∥平面CDE 取DC的中點H,連AH、EH∵G為△ADC的重心,∴G在AH上,且AG=2GH,連FG,則FG∥EH又∵FG![]() 平面CDE, EH
平面CDE, EH![]() 平面CDE,∴GF∥平面CDE
平面CDE,∴GF∥平面CDE


 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
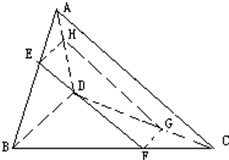 如圖,要在呈空間四邊形的支架上安裝一塊矩形的太陽能吸光板(圖中EFGH),矩形的四個頂點分別在空間四邊形ABCD的邊上.已知AC=a,BD=b,試問:E、F、G、H分別在什么位置時,吸光板的面積最大?
如圖,要在呈空間四邊形的支架上安裝一塊矩形的太陽能吸光板(圖中EFGH),矩形的四個頂點分別在空間四邊形ABCD的邊上.已知AC=a,BD=b,試問:E、F、G、H分別在什么位置時,吸光板的面積最大?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com