
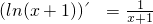 ).
).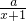 =
=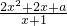 =
=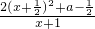 ,
, 時,f′(x)>0,f(x)在(-1,+∞)上單調遞增;
時,f′(x)>0,f(x)在(-1,+∞)上單調遞增; 時,f′(x)=0有兩個解,
時,f′(x)=0有兩個解,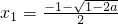 ,
,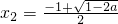 ,且x1<x2,
,且x1<x2, 時,-1<x1<x2,此時f(x)在(-1,x1),(x2,+∞)上單調遞增,在(x1,x2)上單調遞減;
時,-1<x1<x2,此時f(x)在(-1,x1),(x2,+∞)上單調遞增,在(x1,x2)上單調遞減; 時f(x)有兩個極值點,
時f(x)有兩個極值點,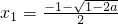 ,
,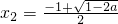 ,x1<x2,
,x1<x2,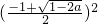 +aln(
+aln(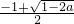 +1),令t=
+1),令t= ,0<t<1,a=
,0<t<1,a=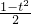 ,
,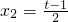 ,
, +
+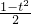 ln
ln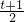 ,令g(t)=
,令g(t)= +
+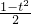 ln
ln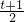 (0<t<1),g′(t)=-tln
(0<t<1),g′(t)=-tln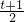 >0,
>0, +
+ <g(t)<0,
<g(t)<0, +
+ ,0).
,0).

 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:
| 1 | x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| n+1 |
| n |
| n-1 |
| n3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com