
【題目】
(1)求 ![]() 的值;
的值;
(2)設m , n![]() N* , n≥m , 求證:
N* , n≥m , 求證:![]() .
.
【答案】
(1)
解: ![]()
(2)
解:對任意的 ![]() ,
,
① 當 ![]() 時,左邊
時,左邊 ![]() ,右邊
,右邊 ![]() ,等式成立,
,等式成立,
② 假設 ![]() 時命題成立,
時命題成立,
即 ![]() ,
,
當 ![]() 時,
時,
左邊= ![]()
![]() ,
,
右邊 ![]() ,
,
而 ![]() ,
,
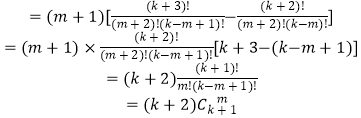
因此 ![]() ,
,
因此左邊=右邊,
因此 ![]() 時命題也成立,
時命題也成立,
綜合①②可得命題對任意 ![]() 均成立.
均成立.
另解:因為 ![]() ,所以
,所以
左邊 ![]()
![]()
又由 ![]() ,知
,知 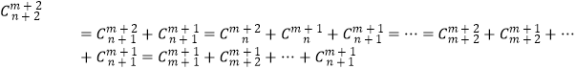 ,
,
所以,左邊 ![]() 右邊.
右邊.
【解析】(1)由已知直接利用組合公式能求出7 ![]() 的值.(2)對任意m∈N* , 當n=m時,驗證等式成立;再假設n=k(k≥m)時命題成立,推導出當n=k+1時,命題也成立,由此利用數學歸納法能證明(m+1)C
的值.(2)對任意m∈N* , 當n=m時,驗證等式成立;再假設n=k(k≥m)時命題成立,推導出當n=k+1時,命題也成立,由此利用數學歸納法能證明(m+1)C ![]() +(m+2)C
+(m+2)C ![]() +(m+3)C
+(m+3)C ![]() +…+nC
+…+nC ![]() +(n+1)C
+(n+1)C ![]() =(m+1)C
=(m+1)C ![]() .
.
【考點精析】通過靈活運用組合與組合數的公式,掌握從n個不同的元素中任取m(m≤n)個元素并成一組,叫做從n個不同元素中取出m個元素的一個組合即可以解答此題.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】α、β是兩個平面,m、n是兩條直線,有下列四個命題:
①如果m⊥n , m⊥α , n∥β , 那么α⊥β.
②如果m⊥α , n∥α , 那么m⊥n.
③如果α∥β , m ![]() α , 那么m∥β.
α , 那么m∥β.
④如果m∥n , α∥β , 那么m與α所成的角和n與β所成的角相等.
其中正確的命題有.(填寫所有正確命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
(1)設a=2,b= ![]() .
.
①求方程f(x)=2的根;
②若對于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求實數m的最大值;
(2)若0<a<1,b>1,函數g(x)=f(x)﹣2有且只有1個零點,求ab的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,點E為棱PC的中點.

(1)證明:BE⊥DC;
(2)求直線BE與平面PBD所成角的正弦值;
(3)若F為棱PC上一點,滿足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x3﹣ax﹣b,x∈R,其中a,b∈R.
(1)求f(x)的單調區間;
(2)若f(x)存在極值點x0 , 且f(x1)=f(x0),其中x1≠x0 , 求證:x1+2x0=0;
(3)設a>0,函數g(x)=|f(x)|,求證:g(x)在區間[﹣1,1]上的最大值不小于 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
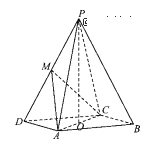
【題目】在四棱錐P-ABC中,底面ABCD為平行四邊形,![]() ,O為AC的中點,
,O為AC的中點,![]() 平面
平面![]() M為PD的中點。
M為PD的中點。
(1)證明![]() 平面
平面![]() .
.
(2)證明![]() 平面
平面![]() .
.
(3)求三棱錐P-MAC體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
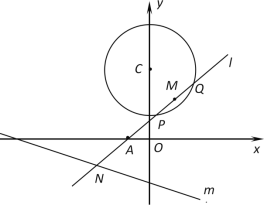
【題目】已知圓![]() :
:![]() ,一動直線l過
,一動直線l過![]() 與圓
與圓![]() 相交于
相交于![]() .兩點,
.兩點,![]() 是
是![]() 中點,l與直線m:
中點,l與直線m:![]() 相交于
相交于![]() .
.
(1)求證:當l與m垂直時,l必過圓心![]() ;
;
(2)當![]() 時,求直線l的方程;
時,求直線l的方程;
(3)探索![]() 是否與直線l的傾斜角有關,若無關,請求出其值;若有關,請說明理由.
是否與直線l的傾斜角有關,若無關,請求出其值;若有關,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com