某同學將命題“在等差數列{an}中,若p+m=2n,則有ap+am=2an(p,m,n∈N*)”改寫成:“在等差數列{an}中,若1×p+1×m=2×n,則有1×ap+1×am=2×an(p,m,n∈N*)”,進而猜想:“在等差數列{an}中,若2p+3m=5n,則有2ap+3am=5an(p,m,n∈N*).”
(1)請你判斷以上同學的猜想是否正確,并說明理由;
(2)請你提出一個更一般的命題,使得上面這位同學猜想的命題是你所提出命題的特例,并給予證明.
(3)請類比(2)中所提出的命題,對于等比數列{bn},請你寫出相應的命題,并給予證明.
【答案】
分析:(1)利用等差數列的通項公式,可把2a
p,3a
m,5a
n都用a
1和d表示,化簡即可得到2a
p+3a
m=5a
n(p,m,n∈N
*).
(2)解法一:可以把(1)中具體的數2,3,5用參數s,t,以及s+t代替,就可得到一個更一般的命題,同樣用等差數列的通項公式,把數列中的每一項用a
1和d表示,化簡即可證明.
解法二:可把(1)中左,右邊兩項推廣到多項相加,只要項的前面系數和相等,就有項之和相等,同樣用用等差數列的通項公式,把數列中的每一項用a
1和d表示,化簡即可證明.
(3)解法一:類比等差數列的性質,得到等比數列的性質,就是把等差數列中的差變為商,和變為積,n倍變為n次方,即可把(2)中解法一類比過去.證明可以用等比數列的通項公式,把數列中的每一項用a
1和q表示,再化簡即可.
解法二:和解法一一樣,把(2)中解法二類比過去,用等比數列的通項公式,把數列中的每一項用a
1和q表示,再化簡即可.
解答:解:(1)命題“在等差數列{a
n}中,若2p+3m=5n,則有2a
p+3a
m=5a
n(p,m,n∈N
*)”正確.
證明:設等差數列{a
n}的首項為a
1,公差為d,由2p+3m=5n得:2a
p+3a
m=2[a
1+(p-1)d]+3[a
1+(m-1)d]=5a
1+d(2p+3m-5)=5a
1+5(n-1)d=5[a
1+(n-1)d]=5a
n,所以命題成立.
(2)解法一:在等差數列{a
n}中,若sp+tm=kn,s+t=k,則有sa
p+ta
m=ka
n(s,t,k,p,m,n∈N
*).顯然,當s=2,t=3,k=5時為以上某同學的猜想.
證明:設等差數列{a
n}的首項為a
1,公差為d,由sp+tm=kn,s+t=k得sa
p+ta
m=s[a
1+(p-1)d]+t[a
1+(m-1)d]=(s+t)a
1+d(sp+tm-s-t)=ka
1+d(kn-k)=k[a
1+(n-1)d]=ka
n,所以命題成立.
(3)解法一:在等比數列{b
n}中,
若sp+tm=kn,s+t=k,則有b
ps•b
mt=b
nk(s,t,k,p,m,n∈N
*).
證明:設等比數列{b
n}的首項為b
1,公比為q,由sp+tm=kn,s+t=k(s,t,k,p,m,n∈N
*)得,b
ps•b
mt=(b
1q
p-1)
s•(b
1q
m-1)
t=b
1s+tq
ps+mt-(s+t)=b
1kq
k(n-1)=(b
1q
n-1)
k=b
nk,所以命題成立.
(2)解法二:在等差數列{a
n}中,若m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t,則有
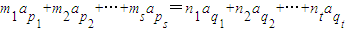
(m
1,m
2,…,m
s,n
1,n
2,…,n
t,p
1,p
2,…,p
s,q
1,q
2,…,q
t∈N
*).
顯然,當s=2,t=1,m
1=2,m
2=3,n
1=5,p=p
1,m=p
2,n=q
1時為某同學的猜想
證明:設等差數列{a
n}的首項為a
1,公差為d,由m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t得
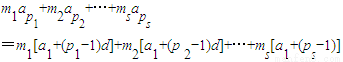
=(m
1+m
2+…+m
s)a
1-(m
1+m
2+…+m
s)d+(m
1p
1+m
2p
2+…+m
sp
s)d
=(n
1+n
2+…+n
t)a
1-(n
1+n
2+…+n
t)d+(n
1q
1+n
2q
2+…+n
tq
t)d
=n
1[a
1+(q
1-1)d]+n
2[a
2+(q
2-1)d]+…+n
s[a
1+(q
s-1)]
=
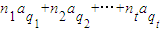
,所以命題成立.
(3)解法二:在等比數列{b
n}中,若m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t,,則有
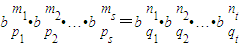
(m
1,m
2,…,m
s,n
1,n
2,…,n
t,p
1,p
2,…,p
s,q
1,q
2,…,q
t∈N
*).
證明:設等比數列{b
n}的首項為b
1,公比為q,由m
1+m
2+…+m
s=n
1+n
2+…+n
t,且m
1p
1+m
2p
2+…+m
sp
s=n
1q
1+n
2q
2+…+n
tq
t得,
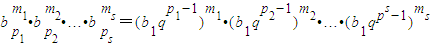
=
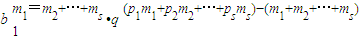

=
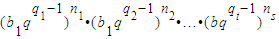
=
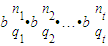
,所以命題成立.
點評:本題主要考查了應用等差數列,等比數列的通項公式證明等差,等比數列的性質.

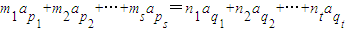
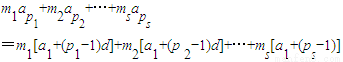 =(m1+m2+…+ms)a1-(m1+m2+…+ms)d+(m1p1+m2p2+…+msps)d
=(m1+m2+…+ms)a1-(m1+m2+…+ms)d+(m1p1+m2p2+…+msps)d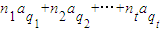 ,所以命題成立.
,所以命題成立. 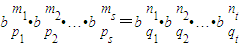
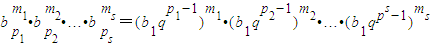 =
=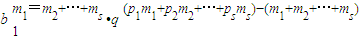

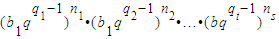 =
=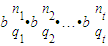 ,所以命題成立.
,所以命題成立.

 科學實驗活動冊系列答案
科學實驗活動冊系列答案![]() 中,若
中,若![]() ,則有
,則有![]() (
(![]() )”改寫成:“在等差數列
)”改寫成:“在等差數列![]() 中,若
中,若![]() ,則有
,則有![]() (
(![]() )”,進而猜想:“在等差數列
)”,進而猜想:“在等差數列![]() 中,若
中,若![]() ,則有
,則有![]() (
(![]() ).”
).”![]() ,請你寫出相應的命題,并給予證明.
,請你寫出相應的命題,并給予證明.![]() 中,若
中,若![]() ,則有
,則有![]() (
(![]() )”改寫成:“在等差數列
)”改寫成:“在等差數列![]() 中,若
中,若![]() ,則有
,則有![]() (
(![]() )”,進而猜想:“在等差數列
)”,進而猜想:“在等差數列![]() 中,若
中,若![]() ,則有
,則有![]() (
(![]() ).”
).”![]() ,請你寫出相應的命題,并給予證明.
,請你寫出相應的命題,并給予證明.