
【題目】已知橢圓![]() :
: ![]() (
(![]() )的右焦點在直線
)的右焦點在直線![]() :
: ![]() 上,且橢圓上任意兩個關于原點對稱的點與橢圓上任意一點的連線的斜率之積為
上,且橢圓上任意兩個關于原點對稱的點與橢圓上任意一點的連線的斜率之積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 經過點
經過點![]() ,且與橢圓
,且與橢圓![]() 有兩個交點
有兩個交點![]() ,
, ![]() ,是否存在直線
,是否存在直線![]() :
: ![]() (其中
(其中![]() )使得
)使得![]() ,
, ![]() 到
到![]() 的距離
的距離![]() ,
, ![]() 滿足
滿足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:
【題目】某學校為倡導全體學生為特困學生捐款,舉行“一元錢,一片心,誠信用水”活動,學生在購水處每領取一瓶礦泉水,便自覺向捐款箱中至少投入一元錢。現統計了連續5天的售出和收益情況,如下表:
售出水量x(單位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(單位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x與y成線性相關,則某天售出8箱水時,預計收益為多少元?
(Ⅱ) 期中考試以后,學校決定將誠信用水的收益,以獎學金的形式獎勵給品學兼優的特困生,規定:特困生考入年級前200名,獲一等獎學金500元;考入年級201—500 名,獲二等獎學金300元;考入年級501名以后的特困生將不獲得獎學金。甲、乙兩名學生獲一等獎學金的概率均為![]() ,獲二等獎學金的概率均為
,獲二等獎學金的概率均為![]() ,不獲得獎學金的概率均為
,不獲得獎學金的概率均為![]() .
.
⑴在學生甲獲得獎學金條件下,求他獲得一等獎學金的概率;
⑵已知甲、乙兩名學生獲得哪個等第的獎學金是相互獨立的,求甲、乙兩名學生所獲得獎學金總金額X 的分布列及數學期望。
附: 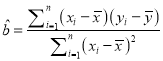 ,
, ![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x)=(ax2+x﹣1)ex
(1)當a<0時,求f(x)的單調區間;
(2)若a=﹣1,f(x)的圖象與g(x)= ![]() x3+
x3+ ![]() x2+m的圖象有3個不同的交點,求實數m的范圍.
x2+m的圖象有3個不同的交點,求實數m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC點,F棱AC上,且AF=3FC. 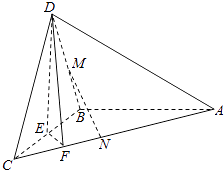
(1)求三棱錐D﹣ABC的體積;
(2)求證:AC⊥平面DEF;
(3)若M為DB中點,N在棱AC上,且CN= ![]() CA,求證:MN∥平面DEF.
CA,求證:MN∥平面DEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
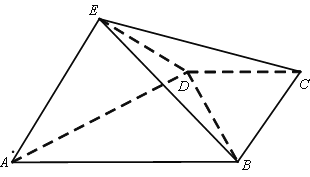
【題目】如圖,已知多面體![]() 的底面
的底面![]() 是邊長為2的正方形,
是邊長為2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)記線段![]() 的中點為
的中點為![]() ,在平面
,在平面![]() 內過點
內過點![]() 作一條直線與平面
作一條直線與平面![]() 平行,要求保留作圖痕跡,但不要求證明.
平行,要求保留作圖痕跡,但不要求證明.
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】制定投資計劃時,不僅要考慮可能獲得的盈利,而且要考慮可能出現的虧損.某投資人打算投資甲、乙兩個項目.根據預測,甲、乙項目可能的最大盈利率分別為100%和50%,可能的最大虧損分別為30%和10%.投資人計劃投資金額不超過10萬元,要求確保可能的資金虧損不超過1.8萬元.問投資人對甲、乙兩個項目各投資多少萬元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+)(ω>0,0≤≤π)為偶函數,其圖象上相鄰的兩個最高點之間的距離為2π. (Ⅰ)求f(x)的解析式;
(Ⅱ)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,
,![]() //
// ![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)求![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() 使得平面
使得平面![]()
![]() 平面
平面![]() ,請說明理由.
,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com