
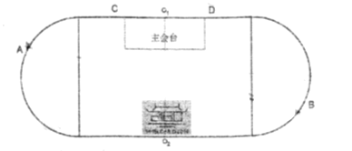
【題目】公元2019年,石室2160歲!文翁興學2160周年紀念活動于2019年11月9日在石室中學文廟校區運動場隆重召開,會場是由一個長![]() ,寬
,寬![]() 的長方形及兩個以長方形寬為直徑的半圓相接組成,整個會場關于中軸線
的長方形及兩個以長方形寬為直徑的半圓相接組成,整個會場關于中軸線![]() 對稱,圖形如下.
對稱,圖形如下.
(1)若![]() 、
、![]() 兩位同學分別在左右兩個半圓弧上值勤,則
兩位同學分別在左右兩個半圓弧上值勤,則![]() 、
、![]() 兩位同學在圓弧什么位置時相距最遠,距離為多少?并說明原因.
兩位同學在圓弧什么位置時相距最遠,距離為多少?并說明原因.
(2)在(1)問的情況下,若要在主會臺后的會場邊界上關于中軸線對稱的兩點![]() 、
、![]() 處分別放置兩個音響,為了達到最好聽覺效果,兩個音響的距離要足夠大,同時
處分別放置兩個音響,為了達到最好聽覺效果,兩個音響的距離要足夠大,同時![]() 、
、![]() 兩位同學聽到兩個音響傳來的聲音時間差不超過0.18秒,求音響距中軸線距離約為多少時為最佳放置點.(注:不超過0.18秒以
兩位同學聽到兩個音響傳來的聲音時間差不超過0.18秒,求音響距中軸線距離約為多少時為最佳放置點.(注:不超過0.18秒以![]() 秒計算,聲音在空氣中的傳播速度為
秒計算,聲音在空氣中的傳播速度為![]() ).
).
【答案】(1)![]() 、
、![]() 兩點分別在圓弧的中點,最遠距離為
兩點分別在圓弧的中點,最遠距離為![]()
![]() ;
;
(2)音響距中軸線距離約為![]() 時為最佳放置點;
時為最佳放置點;
【解析】
(1)分別取兩半圓的圓心為![]() 。根據題意
。根據題意![]() ,利用三角形的性質可證出.
,利用三角形的性質可證出.
(2)以![]() 所在的直線為
所在的直線為![]() 軸, 以中軸線
軸, 以中軸線![]() 為
為![]() 軸建立平面直角坐標系,求出
軸建立平面直角坐標系,求出![]() ,
,
利用雙曲線的定義可得![]() ,設雙曲線方程為
,設雙曲線方程為![]() ,將點
,將點![]() 代入方程,從而求出
代入方程,從而求出![]() ,進而求出
,進而求出![]() 即可求解.
即可求解.
(1)分別取兩半圓的圓心為![]()
由題意可得![]()
當![]() 四點共線時,
四點共線時,![]() 、
、![]() 兩點間的距離最大,
兩點間的距離最大,
此時![]() 、
、![]() 兩點分別在圓弧的中點,距離為
兩點分別在圓弧的中點,距離為![]()
![]()
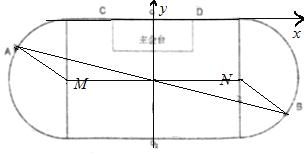
(2)以![]() 所在的直線為
所在的直線為![]() 軸, 以中軸線
軸, 以中軸線![]() 為
為![]() 軸建立平面直角坐標系,
軸建立平面直角坐標系,
則 ![]() ,
,![]()
根據題意可得![]() ,
,
![]() 、
、![]() 兩點在以
兩點在以![]() 為焦點的雙曲線上,
為焦點的雙曲線上, ![]() ,即
,即![]() ,
,
設雙曲線方程為:![]() ,則
,則![]() ,解得
,解得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即音響距中軸線距離約為![]() 時為最佳放置點.
時為最佳放置點.


科目:高中數學 來源: 題型:
【題目】黨的十九大明確把精準脫貧作為決勝全面建成小康社會必須打好的三大攻堅戰之一.為堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村脫貧,堅持扶貧同扶智相結合,此幫扶單位考察了甲、乙兩種不同的農產品加工生產方式,現對兩種生產方式的產品質量進行對比,其質量按測試指標可劃分為:指標在區間![]() 的為優等品;指標在區間
的為優等品;指標在區間![]() 的為合格品,現分別從甲、乙兩種不同加工方式生產的農產品中,各自隨機抽取100件作為樣本進行檢測,測試指標結果的頻數分布表如下:
的為合格品,現分別從甲、乙兩種不同加工方式生產的農產品中,各自隨機抽取100件作為樣本進行檢測,測試指標結果的頻數分布表如下:
甲種生產方式:
指標區間 |
|
|
|
|
|
|
頻數 | 5 | 15 | 20 | 30 | 15 | 15 |
乙種生產方式:
指標區間 |
|
|
|
|
|
|
頻數 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲種方式生產的產品中,按合格品與優等品用分層抽樣方式,隨機抽出5件產品,①求這5件產品中,優等品和合格品各多少件;②再從這5件產品中,隨機抽出2件,求這2件中恰有1件是優等品的概率;
(2)所加工生產的農產品,若是優等品每件可售55元,若是合格品每件可售25元.甲種生產方式每生產一件產品的成本為15元,乙種生產方式每生產一件產品的成本為20元.用樣本估計總體比較在甲、乙兩種不同生產方式下,該扶貧單位要選擇哪種生產方式來幫助該扶貧村來脫貧?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的個數是( )
①從某社區65戶高收入家庭,280戶中等收入家庭,105戶低收入家庭中選出100戶調查社會購買力的某一項指標,應采用的最佳抽樣方法是分層抽樣
②線性回歸直線![]() 一定過樣本中心點
一定過樣本中心點![]()
③對于一組數據![]() ,如果將它們改變為
,如果將它們改變為![]() ,則平均數與方差均發生變化
,則平均數與方差均發生變化
④若一組數據1、![]() 、2、3的眾數是2,則這組數據的中位數是2
、2、3的眾數是2,則這組數據的中位數是2
⑤用系統抽樣方法從編號為1,2,3,…,700的學生中抽樣50人,若第2段中編號為20的學生被抽中,按照等間隔抽取的方法,則第5段中被抽中的學生編號為76
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接2022年冬奧會,北京市組織中學生開展冰雪運動的培訓活動,并在培訓結束后對學生進行了考核.記![]() 表示學生的考核成績,并規定
表示學生的考核成績,并規定![]() 為考核優秀.為了了解本次培訓活動的效果,在參加培訓的學生中隨機抽取了30名學生的考核成績,并作成如下莖葉圖:
為考核優秀.為了了解本次培訓活動的效果,在參加培訓的學生中隨機抽取了30名學生的考核成績,并作成如下莖葉圖:

(Ⅰ)從參加培訓的學生中隨機選取1人,請根據圖中數據,估計這名學生考核優秀的概率;
(Ⅱ)從圖中考核成績滿足![]() 的學生中任取2人,求至少有一人考核優秀的概率;
的學生中任取2人,求至少有一人考核優秀的概率;
(Ⅲ)記![]() 表示學生的考核成績在區間
表示學生的考核成績在區間![]() 的概率,根據以往培訓數據,規定當
的概率,根據以往培訓數據,規定當![]() 時培訓有效.請根據圖中數據,判斷此次中學生冰雪培訓活動是否有效,并說明理由.
時培訓有效.請根據圖中數據,判斷此次中學生冰雪培訓活動是否有效,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 與
與![]() 的中心在坐標原點
的中心在坐標原點![]() ,長軸均為
,長軸均為![]() 且在
且在![]() 軸上,短軸長分別為
軸上,短軸長分別為![]() ,
,![]() ,過原點且不與
,過原點且不與![]() 軸重合的直線
軸重合的直線![]() 與
與![]() ,
,![]() 的四個交點按縱坐標從大到小依次為
的四個交點按縱坐標從大到小依次為![]() ,記
,記![]() ,
,![]() 和
和![]() 的面積分別為
的面積分別為![]() 和
和![]() .
.
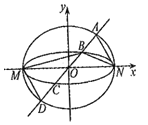
(1)當直線![]() 與
與![]() 軸重合時,若
軸重合時,若![]() ,求
,求![]() 的值;
的值;
(2)當![]() 變化時,是否存在與坐標軸不重合的直線
變化時,是否存在與坐標軸不重合的直線![]() ,使得
,使得![]() ?并說明理由.
?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 截直線
截直線![]() 所得線段的中點坐標為
所得線段的中點坐標為![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)=![]() 若不建隔熱層,每年能源消耗費用為8萬元。設f(x)為隔熱層建造費用與20年的能源消耗費用之和。
若不建隔熱層,每年能源消耗費用為8萬元。設f(x)為隔熱層建造費用與20年的能源消耗費用之和。
(Ⅰ)求k的值及f(x)的表達式。
(Ⅱ)隔熱層修建多厚時,總費用f(x)達到最小,并求最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com