
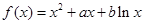 (
(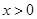 ,實數(shù)
,實數(shù)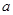 ,
,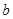 為常數(shù)).
為常數(shù)).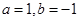 ,求
,求 在
在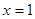 處的切線方程;
處的切線方程;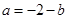 ,討論函數(shù)
,討論函數(shù) 的單調性.
的單調性.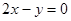 ;
;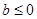 時,函數(shù)
時,函數(shù) 的單調遞減區(qū)間為
的單調遞減區(qū)間為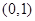 ,單調遞增區(qū)間為
,單調遞增區(qū)間為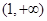 ;當
;當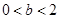 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為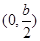 ,
,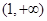 ,單調遞減區(qū)間為
,單調遞減區(qū)間為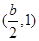 ;當
;當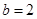 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為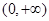 ;當
;當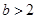 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為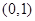 ,
,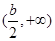 ,單調遞減區(qū)間為
,單調遞減區(qū)間為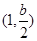 .
.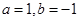 ,代入
,代入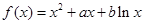 ,可求出
,可求出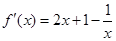 ,當
,當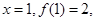
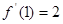 ,由點斜式方程寫出曲線的切線方程,再化為一般式;(2)把
,由點斜式方程寫出曲線的切線方程,再化為一般式;(2)把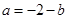 代入得
代入得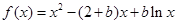 ,
,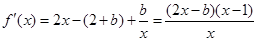 ,注意定義域,令
,注意定義域,令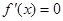 ,得
,得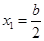 ,
,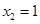 .需討論
.需討論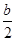 與0和1的大小得
與0和1的大小得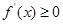 或
或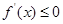 的
的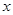 的范圍,就是原函數(shù)的增區(qū)間或減區(qū)間.
的范圍,就是原函數(shù)的增區(qū)間或減區(qū)間.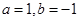 ,所以函數(shù)
,所以函數(shù)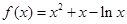 ,
,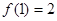
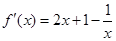 ,
,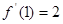 ………………………………………………2分
………………………………………………2分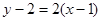
 在
在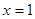 處的切線方程為
處的切線方程為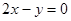 …………………………………5分
…………………………………5分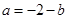 ,所以
,所以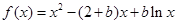 ,則
,則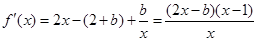
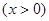
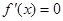 ,得
,得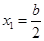 ,
,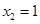 .……………………………………………7分
.……………………………………………7分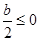 ,即
,即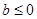 時,函數(shù)
時,函數(shù) 的單調遞減區(qū)間為
的單調遞減區(qū)間為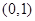 ,
,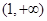 ;…………………………………………8分
;…………………………………………8分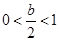 ,即
,即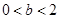 時,
時,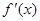 ,
, 的變化情況如下表:
的變化情況如下表: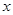 | 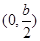 | 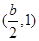 | 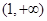 |
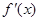 | 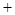 | 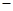 | 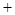 |
 |  |  |  |
 的單調遞增區(qū)間為
的單調遞增區(qū)間為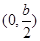 ,
,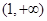 ,
,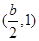 ;…………………………9分
;…………………………9分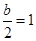 ,即
,即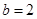 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為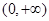 ;………10分
;………10分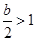 ,即
,即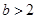 時,
時,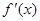 ,
, 的變化情況如下表:
的變化情況如下表: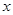 | 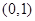 | 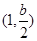 | 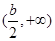 |
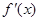 | 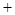 | 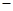 | 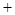 |
 |  |  |  |
 的單調遞增區(qū)間為
的單調遞增區(qū)間為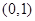 ,
,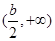 ,單調遞減區(qū)間為
,單調遞減區(qū)間為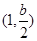 ;……………………………………11分
;……………………………………11分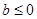 時,函數(shù)
時,函數(shù) 的單調遞減區(qū)間為
的單調遞減區(qū)間為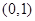 ,單調遞增區(qū)間為
,單調遞增區(qū)間為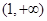 ;當
;當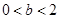 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為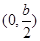 ,
,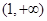 ,單調遞減區(qū)間為
,單調遞減區(qū)間為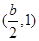 ;當
;當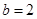 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為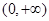 ;當
;當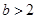 時,函數(shù)
時,函數(shù) 的單調遞增區(qū)間為
的單調遞增區(qū)間為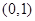 ,
,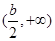 ,單調遞減區(qū)間為
,單調遞減區(qū)間為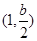 .…………………………12分
.…………………………12分

科目:高中數(shù)學 來源:不詳 題型:解答題
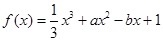 (
(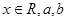 為實數(shù))有極值,且在
為實數(shù))有極值,且在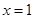 處的切線與直線
處的切線與直線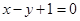 平行.
平行.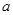 的取值范圍;
的取值范圍;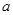 ,使得函數(shù)
,使得函數(shù)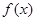 的極小值為1,若存在,求出實數(shù)
的極小值為1,若存在,求出實數(shù)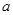 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;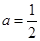 ,
,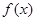 的導數(shù)為
的導數(shù)為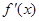 ,令
,令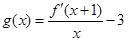
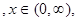
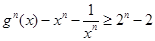
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com