【題目】已知點
,
是函數
圖象上的任意兩點,且角
的終邊經過點
,若
時,
的 最小值為
.
（1）求函數
的解析式；
（2）當
時,不等式
恒成立,求實數
的取值范圍.
【答案】（1）
；（2）
.
【解析】試題分析：（1）利用三角函數的定義求出
的值，由
時，
的最小值為
，可得函數的周期，從而可求
，進而可求函數
的解析式；（2）當
時，不等式
恒成立，等價于
，先求出得
的最大值，由此可得
的取值范圍.
試題解析：（1）角
的終邊經過點
，
，
，
.
由
時,
的最小值為，得
，即
，
∴
(2）當時,
, 于是,
,
等價于
由 , 得的最大值為
所以，實數的取值范圍是
注：用別的方法求得，只要正確就給3分.
【方法點晴】本題主要考查三角函數圖像與性質及不等式恒成立問題，屬于難題．不等式恒成立問題常見方法：① 分離參數
恒成立(
可)或
恒成立（
即可）；② 數形結合(
圖象在
上方即可)；③ 討論最值
或
恒成立；④ 討論參數.本題是利用方法 ① 求得 的范圍的.
期末100分闖關海淀考王系列答案
小學能力測試卷系列答案科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系中，以坐標原點為極點，
軸為正半軸建立極坐標系，圓
的極坐標方程為
，直線
的參數方程為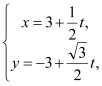
（t為參數）.
（1）求圓的直角坐標方程；
（2）求直線分圓所得的兩弧程度之比.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某飛機失聯，經衛星偵查，其最后出現在小島
附近，現派出四艘搜救船
，為方便聯絡，船
始終在以小島為圓心，100海里為半徑的圓上，船構成正方形編隊展開搜索，小島在正方形編隊外（如圖）.設小島到
的距離為
，
，
船到小島的距離為
.
（1）請分別求關于
的函數關系式
，并分別寫出定義域；
（2）當兩艘船之間的距離是多少時搜救范圍最大（即最大）？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了普及法律知識，達到“法在心中”的目的，某市法制辦組織了普法知識競賽．統計局調查隊隨機抽取了甲、乙兩單位中各5名職工的成績，成績如下表：
甲單位 | 87 | 88 | 91 | 91 | 93 |
乙單位 | 85 | 89 | 91 | 92 | 93 |
（1）根據表中的數據，分別求出甲、乙兩單位職工成績的平均數和方差，并判斷哪個單位對法律知識的掌握更穩定；
（2）用簡單隨機抽樣法從乙單位5名職工中抽取2名，他們的成績組成一個樣本，求抽取的2名職工的分數差至少是4的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
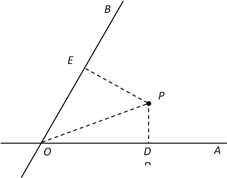
【題目】如圖，
、
是兩條公路（近似看成兩條直線），
，在
內有一紀念塔
（大小忽略不計），已知到直線、的距離分別為
、
，=6千米，=12千米．現經過紀念塔修建一條直線型小路，與兩條公路、分別交于點
、
．
（1）求紀念塔到兩條公路交點
處的距離；
（2）若紀念塔為小路
的中點，求小路的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
（
）.
（1）證明：直線
過定點；
（2）若直線不經過第四象限，求
的取值范圍；
（3）若直線
軸負半軸于
，交
軸正半軸于
，△
的面積為
（
為坐標原點），求的最小值，并求此時直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
