
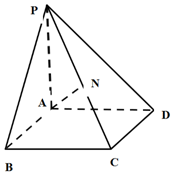
 如圖,已知四邊形ABCD是邊長為1的正方形,PA⊥平面ABCD,N是PC的中點.
如圖,已知四邊形ABCD是邊長為1的正方形,PA⊥平面ABCD,N是PC的中點. 分析 (Ⅰ)四邊性ABCD是邊長為1的正方形,PA⊥平面ABCD,作BM⊥PC,連接MD,可得RT△PBC≌RT△PDC,DM⊥PC,因此∠BMD就是所求二面角的平面角.再利用余弦定理即可得出.
(II)設AN與平面PCD所成角為α,PA=h.作AQ⊥PD,又CD⊥AQ,可得AQ⊥平面PCD,利用直角三角形的邊角關系可得:$sinα=\frac{AQ}{AN}=\sqrt{\frac{{4{h^2}}}{{({1+{h^2}})({2+{h^2}})}}}=\sqrt{\frac{{4{h^2}}}{{{h^4}+3{h^2}+2}}}$,再利用基本不等式的性質即可得出.
解答 解:(Ⅰ)四邊形ABCD是邊長為1的正方形,PA⊥平面ABCD,作BM⊥PC,連接MD,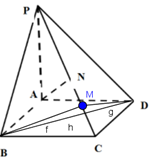
由于RT△PBC≌RT△PDC,
則DM⊥PC,∴∠BMD就是所求二面角的平面角.
PA=AB=1,∴$PB=\sqrt{2},PC=\sqrt{3}$,∴$BM=\frac{{\sqrt{6}}}{3}$.
同理$DM=\frac{{\sqrt{6}}}{3}$,又$BD=\sqrt{2}$,
在△BDM中,
由余弦定理得$cos∠BMD=\frac{{B{M^2}+D{M^2}-B{D^2}}}{2BM•DM}=-\frac{1}{2}$,
二面角B-PC-D的大小為$\frac{2π}{3}$.
(Ⅱ)設AN與平面PCD所成角為α,PA=h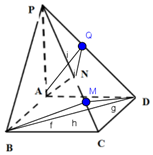 .
.
作AQ⊥PD又CD⊥AQ,∴AQ⊥平面PCD,
因此在RT△AQN中,$sinα=\frac{AQ}{AN}$.
∵在RT△PAD中,$AQ=\frac{h}{{\sqrt{1+{h^2}}}}$,
在RT△PAC中,$AN=\frac{{\sqrt{2+{h^2}}}}{2}$,$sinα=\frac{AQ}{AN}=\sqrt{\frac{{4{h^2}}}{{({1+{h^2}})({2+{h^2}})}}}=\sqrt{\frac{{4{h^2}}}{{{h^4}+3{h^2}+2}}}$,
∵${h^4}+2≥2\sqrt{2{h^4}}=2\sqrt{2}{h^2}$,
$sinα≤\sqrt{\frac{{4{h^2}}}{{2\sqrt{2}{h^2}+3{h^2}}}}=\sqrt{\frac{4}{{3+2\sqrt{2}}}}=\frac{2}{{\sqrt{2}+1}}=2({\sqrt{2}-1})$.
點評 本題考查了空間位置關系與空間角、余弦定理、直角三角形的邊角關系、基本不等式的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (4,+∞) | B. | $[0,\frac{1}{2}]$ | C. | $(\frac{1}{2},4]$ | D. | (1,4] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com