
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(Ⅱ)若在區間![]() 上存在不相等的實數
上存在不相等的實數![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)若函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,求證:
,求證:![]() .
.
【答案】(Ⅰ)函數![]() 的單調增區間為
的單調增區間為![]() ,
,![]() ,單調減區間為
,單調減區間為![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)證明見解析.
;(Ⅲ)證明見解析.
【解析】
試題分析:(Ⅰ)將![]() 代入函數的表達式,求出函數的導數,解關于導函數的不等式,從而求出函數的單調區間;(Ⅱ)問題轉化為求使函數
代入函數的表達式,求出函數的導數,解關于導函數的不等式,從而求出函數的單調區間;(Ⅱ)問題轉化為求使函數![]() 在
在![]() 上不為單調函數的
上不為單調函數的![]() 的取值范圍,通過討論
的取值范圍,通過討論![]() 的范圍,得到函數的單調性,進而求出
的范圍,得到函數的單調性,進而求出![]() 的范圍;(Ⅲ)先求出函數的導數,找到函數的極值點,從而證明出結論.
的范圍;(Ⅲ)先求出函數的導數,找到函數的極值點,從而證明出結論.
試題解析:(Ⅰ)當![]() 時,
時,![]() ,
,![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
當![]() 時,
時,![]() >0,f(x)單調遞增;
>0,f(x)單調遞增;
當![]() 時,
時,![]() <0,f(x)單調遞減;
<0,f(x)單調遞減;
當![]() 時,
時,![]() >0,f(x)單調遞增.
>0,f(x)單調遞增.
所以函數![]() 的單調增區間為
的單調增區間為![]() ,
,![]() ,單調減區間為
,單調減區間為![]()
(Ⅱ)依題意即求使函數![]() 在
在![]() 上不為單調函數的
上不為單調函數的![]() 的取值范圍.
的取值范圍.
![]() .設
.設![]() ,則
,則![]() ,
,![]() .
.
因為函數![]() 在
在![]() 上為增函數,當
上為增函數,當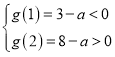 ,
,
即當![]() 時,函數
時,函數![]() 在
在![]() 上有且只有一個零點,設為
上有且只有一個零點,設為![]() .
.
當![]() 時,
時,![]() ,即
,即![]() ,
,![]() 為減函數;
為減函數;
當![]() 時,
時,![]() ,即
,即![]() ,
,![]() 為增函數,
為增函數,
滿足在![]() 上不為單調函數.
上不為單調函數.
當![]() 時,
時,![]() ,
,![]() ,所以在
,所以在![]() 上
上![]() 成立
成立
(因![]() 在
在![]() 上為增函數),所以在
上為增函數),所以在![]() 上
上![]() 成立,
成立,
即![]() 在
在![]() 上為增函數,不合題意.
上為增函數,不合題意.
同理![]() 時,可判斷
時,可判斷![]() 在
在![]() 上為減函數,不合題意.綜上
上為減函數,不合題意.綜上![]()
(Ⅲ) ![]() .
.
因為函數![]() 有兩個不同的極值點,即
有兩個不同的極值點,即![]() 有兩個不同的零點,
有兩個不同的零點,
即方程![]() 的判別式
的判別式![]() ,解得
,解得![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
此時![]() ,
,![]() .
.
隨著![]() 變化時,
變化時,![]() 和
和![]() 的變化情況如下:
的變化情況如下:
|
|
|
|
|
|
| + |
| - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
所以![]() 是函數
是函數![]() 的極大值點,
的極大值點,![]() 是函數
是函數![]() 的極小值點.
的極小值點.
所以![]() 為極大值,
為極大值,![]() 為極小值.
為極小值.
![]() 所以
所以![]()
![]()
![]()
![]()
![]()
因為![]() ,所以
,所以![]() .所以
.所以![]()


科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率
的離心率![]() ,過點
,過點![]() 和
和![]() 的直線與原點的距離為
的直線與原點的距離為![]() .
.

(1)求橢圓的方程;
(2)設![]() 為橢圓的左、右焦點,過
為橢圓的左、右焦點,過![]() 作直線交橢圓于
作直線交橢圓于![]() 兩點,求△
兩點,求△![]() 的內切圓半徑
的內切圓半徑![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把黑、紅、白3張紙牌分給甲、乙、丙三人,則事件“甲分得紅牌”與“乙分得紅牌”是( )
A. 對立事件 B. 互斥但不對立事件
C. 不可能事件 D. 必然事件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱錐P﹣ABCD如圖.
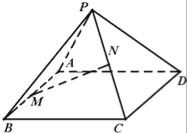
(Ⅰ)若其正視圖是一個邊長分別為![]() 、
、![]() ,2的等腰三角形,求其表面積S、體積V;
,2的等腰三角形,求其表面積S、體積V;
(Ⅱ)設AB中點為M,PC中點為N,證明:MN∥平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】6月23日15時前后,江蘇鹽城市阜寧、射陽等地突遭強冰雹、龍卷風雙重災害襲擊,風力達12級.災害發生后,有甲、乙、丙、丁4個輕型救援隊從A,B,C,D四個不同的方向前往災區.已知下面四種說法都是正確的.
(1)甲輕型救援隊所在方向不是C方向,也不是D方向;
(2)乙輕型救援隊所在方向不是A方向,也不是B方向;
(3)丙輕型救援隊所在方向不是A方向,也不是B方向;
(4)丁輕型救援隊所在方向不是A方向,也不是D方向;
此外還可確定:如果丙所在方向不是D方向,那么甲所在方向就不是A方向,有下列判斷:
①甲所在方向是B方向;②乙所在方向是D方向;③丙所在方向是D方向;④丁所在方向是C方向.
其中判斷正確的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了了解全校學生的上網情況,在全校采用隨機抽樣的方法抽取了40名學生(其中男女生人數恰好各占一半)進行問卷調查,并進行了統計,按男女分為兩組,再將每組學生的月上網次數分為5組:![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:

(I)寫出![]() 的值;
的值;
(II)在抽取的40名學生中,從月上網次數不少于20次的學生中隨機抽取3人,并用![]() 表示其中男生的人數,求
表示其中男生的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校做了一次關于“感恩父母”的問卷調查,從8~10歲,11~12歲,13~14歲,15~16歲四個年齡段回收的問卷依次為:120份,180份,240份,x份.因調查需要,從回收的問卷中按年齡段分層抽取容量為300的樣本,其中在11~12歲學生問卷中抽取60份,則在15~16歲學生中抽取的問卷份數為( )
A.60 B.80 C.120 D.180
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com