若函數f(x)=x2+ax+b的兩個零點是-2和3,則不等式af(-2x)>0的解集是 .
【答案】
分析:由已知函數f(x)=x
2+ax+b的兩個零點是-2和3得a,b的值,不等式af(-2x)>0,即為常見的一元二次不等式,解之即得.
解答:解:∵f(x)=x
2+ax+b的兩個零點是-2,3.
∴-2,3是方程x
2+ax+b=0的兩根,
由根與系數的關系知
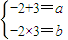
,∴
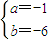
,
∴f(x)=x
2-x-6.
∵不等式a?(-2x)>0,即-(4x
2+2x-6)>0
?2x
2+x-3<0,
解集為

.
故答案為
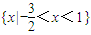 點評:
點評:此題體現了一元二次不等式的解法,解決一元二次不等式的解法的問題,常常需要向方程或圖象方面轉化,而數形結合正是它們轉化的紐帶,求解不等式聯系方程的根,不等中隱藏著相等.
