
 如圖所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F為CE上的點,且BF⊥平面ACE
如圖所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F為CE上的點,且BF⊥平面ACE| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |


科目:高中數學 來源: 題型:
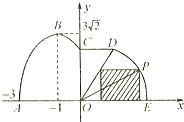 如圖,某市擬在道路的一側修建一條運動賽道,賽道的前一部分為曲線段ABC,該曲線段為函數y=Asin(ωx+φ)(A>0,ω>0,
如圖,某市擬在道路的一側修建一條運動賽道,賽道的前一部分為曲線段ABC,該曲線段為函數y=Asin(ωx+φ)(A>0,ω>0,| π |
| 2 |
| 2 |
| 3 |
 |
| DE |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,在△ABC中,AC=1,AB=3,∠ACB=
如圖所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,在△ABC中,AC=1,AB=3,∠ACB=
如圖所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中數學 來源:2011年江蘇省南京市金陵中學高考數學預測試卷(2)(解析版) 題型:解答題
 <φ<π),x∈[-3,0]的圖象,且圖象的最高點為B(-1,3
<φ<π),x∈[-3,0]的圖象,且圖象的最高點為B(-1,3 );賽道的中間部分為
);賽道的中間部分為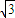 千米的水平跑到CD;賽道的后一部分為以O圓心的一段圓弧
千米的水平跑到CD;賽道的后一部分為以O圓心的一段圓弧 .
.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省高三預測卷2數學 題型:解答題
(本小題滿分14分)
如圖,某市擬在道路的一側修建一條運動賽道,賽道的前一部分為曲線段ABC,該曲線段為函數y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的圖象,且圖象的最高點為B(-1,
),x∈[-3,0]的圖象,且圖象的最高點為B(-1, );賽道的中間部分為
);賽道的中間部分為 千米的水平跑到CD;賽道的后一部分為以O圓心的一段圓弧
千米的水平跑到CD;賽道的后一部分為以O圓心的一段圓弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圓弧賽道所對應的扇形區域內建一個“矩形草坪”,如圖所示,矩形的一邊在道路AE上,一個頂點在扇形半徑OD上.記∠POE= ,求當“矩形草坪”的面積最大時
,求當“矩形草坪”的面積最大時 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com