
���}Ŀ����֪�A![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() .
.
��1��������![]() ������c�A
������c�A![]() ������(sh��)��(sh��)
���У���(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2���^(gu��)ֱ��![]() �ϵ��c(di��n)
�ϵ��c(di��n)![]() ���A
���A![]() �ăɗl�о������c(di��n)��
�ăɗl�о������c(di��n)��![]() ����
����![]() ���t�Q�c(di��n)
���t�Q�c(di��n)![]() �������c(di��n)��. ��ֱ��
�������c(di��n)��. ��ֱ��![]() ������ֻ�Ѓɂ�(g��)�����c(di��n)������(sh��)��(sh��)
������ֻ�Ѓɂ�(g��)�����c(di��n)������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1�����![]() �����c(di��n)����(bi��o)��ֱ��
�����c(di��n)����(bi��o)��ֱ��![]() ��б�ʣ��ɵ�
��б�ʣ��ɵ�![]() ���д������̣�����ֱ���c�A���У����
���д������̣�����ֱ���c�A���У����![]() ���ɣ�
���ɣ�
��2���B��![]() ��������A
��������A![]() �ķ��̣�ֱ��
�ķ��̣�ֱ��![]() ������ֻ�Ѓɂ�(g��)�����c(di��n)�����Ƴ��A��
������ֻ�Ѓɂ�(g��)�����c(di��n)�����Ƴ��A��![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ����⼴�ɣ�
����⼴�ɣ�
�⣺��1����![]() ��
��![]() �ã�
�ã�
![]() �����c(di��n)����(bi��o)��
�����c(di��n)����(bi��o)��![]() ��ֱ��
��ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��
����![]() ���д������̞�
���д������̞�![]() ����
����![]() ��
��
����?y��n)?/span>![]() ������c�A
������c�A![]() ����
����
���ԈA��![]() ��
��![]() �д����ľ��x
�д����ľ��x![]() ��
��
��![]() ��
��
��2���B��![]() ��
��
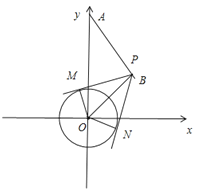
��![]() ��
��![]() ��
��![]() ��
��
����![]() ��
��
�����c(di��n)![]() ��܉�E����
��܉�E����![]() ��A�ģ�
��A�ģ�![]() ��돽�ĈA��ӛ��A
��돽�ĈA��ӛ��A![]() ��
��
�t�A![]() �ķ��̞�
�ķ��̞�![]() ��
��
����?y��n)�ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����ֱ��
����ֱ��![]() ������ֻ�Ѓɂ�(g��)�����c(di��n)����
������ֻ�Ѓɂ�(g��)�����c(di��n)����
�tֱ��![]() �c�A
�c�A![]() �ཻ��
�ཻ��
���ԈA��![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ��
��
�ʌ�(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������![]() .
.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�(xi��ng)��(sh��)��![]() �(xi��ng)���иF��(sh��)��
�(xi��ng)���иF��(sh��)��![]() ����ͬ�r(sh��)�M����������(g��)�l����
����ͬ�r(sh��)�M����������(g��)�l����
![]() ��
��![]() ��������(sh��)
��������(sh��)![]() ��
��![]() ��1������
��1������![]() ��3��
��3��![]() ��
��![]() ��
��
![]() ��ȡ��(sh��)��
��ȡ��(sh��)��![]() �еă��(xi��ng)
�еă��(xi��ng)![]() ��
��![]() ��ʣ�µ�
��ʣ�µ�![]() �(xi��ng)��һ�����ڃ��(xi��ng)
�(xi��ng)��һ�����ڃ��(xi��ng)![]() ��
��![]() ���M��
���M��![]() ���t�Q��(sh��)��
���t�Q��(sh��)��![]() ��
��![]() ��(sh��)��
��(sh��)��
![]() ����(sh��)��
����(sh��)��![]() �����(xi��ng)��1�������1���(xi��ng)��(sh��)��6�(xi��ng)�ĵȲ(sh��)�У��Д���(sh��)��
�����(xi��ng)��1�������1���(xi��ng)��(sh��)��6�(xi��ng)�ĵȲ(sh��)�У��Д���(sh��)��![]() �Ƿ���
�Ƿ���![]() ��(sh��)�У����f(shu��)�����ɣ�
��(sh��)�У����f(shu��)�����ɣ�
![]() ��(d��ng)
��(d��ng)![]() �r(sh��)���O(sh��)
�r(sh��)���O(sh��)![]() ��(sh��)��
��(sh��)��![]() ��1���F(xi��n)
��1���F(xi��n)![]() ��2���F(xi��n)
��2���F(xi��n)![]() ��3���F(xi��n)
��3���F(xi��n)![]() ������
������![]() ��
��![]() ��
��![]() ��
��
���C��![]() ��
��![]() ��
��![]() ��
��
![]() ��(d��ng)
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ��(sh��)��
��(sh��)��![]() ���(xi��ng)��(sh��)
���(xi��ng)��(sh��)![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij��W(xu��)����4�����I(y��)����ij��I(y��)������(g��)���T![]() ��(sh��)��(x��)��Ҫ��ÿ��(g��)���T���ٰ���1�ˣ����м״�W(xu��)�����ܰ��ŵ�
��(sh��)��(x��)��Ҫ��ÿ��(g��)���T���ٰ���1�ˣ����м״�W(xu��)�����ܰ��ŵ�![]() ���T���������ŷ�����______�N
���T���������ŷ�����______�N![]() �Ô�(sh��)������
��(sh��)������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪�E�A![]() ���x���ʞ�
���x���ʞ�![]() ���Ҝ�(zh��n)�����̞�
���Ҝ�(zh��n)�����̞�![]() ��
��![]() ��
��![]() �քe�ǙE�A
�քe�ǙE�A![]() ��������c(di��n)���^(gu��)�ҽ��c(di��n)
��������c(di��n)���^(gu��)�ҽ��c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n).
���c(di��n).
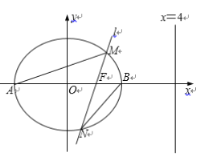
��1����E�A![]() ��(bi��o)��(zh��n)����.
��(bi��o)��(zh��n)����.
��2��ӛ![]() ��
��![]() ����e�քe��
����e�քe��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
��3���O(sh��)����![]() �����c(di��n)��
�����c(di��n)��![]() ��ֱ��
��ֱ��![]() �c�Ҝ�(zh��n)���ཻ���c(di��n)
�c�Ҝ�(zh��n)���ཻ���c(di��n)![]() ��ӛֱ��
��ӛֱ��![]() ��
��![]() ��
��![]() ��б�ʷքe��
��б�ʷքe��![]() ��
��![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��4��(g��)��ͬ�ļt���6��(g��)��ͬ�İ������ͬһ��(g��)���У��F(xi��n)����ȡ��4��(g��)��
��1����ȡ���ļt��Ă�(g��)��(sh��)�����ڰ���Ă�(g��)��(sh��)���t�ж��ٲ�ͬ��ȡ����
��2��ȡ��һ��(g��)�t��ӛ2�֣�ȡ��һ��(g��)����ӛ1�֣���ȡ��4��(g��)�����ÿ��ֲ�����5�֣��t�ж��ٷN��ͬȡ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]() ����g�����l����ƽ���҃Ƀ��g�ľ��x�քe��4��5��6��ֱ�����o����������(g��)�Y(ji��)Փ��
����g�����l����ƽ���҃Ƀ��g�ľ��x�քe��4��5��6��ֱ�����o����������(g��)�Y(ji��)Փ��
�ٴ���![]() ʹ��
ʹ��![]() ��ֱ�������Σ�
��ֱ�������Σ�
�ڴ���![]() ʹ��
ʹ��![]() �ǵ�߅�����Σ�
�ǵ�߅�����Σ�
�����lֱ���ϴ������c(di��n)![]() ʹ�������w
ʹ�������w![]() ����һ��(g��)��c(di��n)̎�����l��Ƀɻ��ഹֱ�������w�����У��������_�Y(ji��)Փ�Ă�(g��)��(sh��)��( )
����һ��(g��)��c(di��n)̎�����l��Ƀɻ��ഹֱ�������w�����У��������_�Y(ji��)Փ�Ă�(g��)��(sh��)��( )
A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ��(g��)���������������ij�Ҫ�l���ǣ� ��
A.������������,�Ѓɂ�(g��)��(c��)���Ǿ���B.������������,�Ѓɂ�(g��)��(c��)�洹ֱ����
C.������������,�����ɂ�(g��)��(c��)���Ǿ���D.ÿ��(g��)��(c��)�涼��ȫ�ȵľ���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��[�x��4-4������(bi��o)ϵ�c����(sh��)����]
������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�����S��O�S�����O����(bi��o)ϵ������
�S�����S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)������
�ĘO����(bi��o)������![]() .
.
��1��������![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)�^(gu��)�c(di��n)![]() �҃Aб�Ǟ�
�҃Aб�Ǟ�![]() ��ֱ��
��ֱ��![]() ������
������![]() ���ڃ��c(di��n)
���ڃ��c(di��n)![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������L(zh��ng)��1�������w![]() �У��c(di��n)
�У��c(di��n)![]() �nj�(du��)�Ǿ�
�nj�(du��)�Ǿ�![]() �ϵĄ�(d��ng)�c(di��n)���c(di��n)
�ϵĄ�(d��ng)�c(di��n)���c(di��n)![]() �c
�c![]() ���غϣ����t���нY(ji��)Փ���_����__________
���غϣ����t���нY(ji��)Փ���_����__________
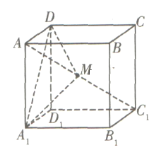
�ٴ����c(di��n)![]() ��ʹ��ƽ��
��ʹ��ƽ��![]() ƽ��
ƽ��![]() ��
��
�ڴ����c(di��n)![]() ��ʹ��ƽ��
��ʹ��ƽ��![]() ƽ��
ƽ��![]() ��
��
��![]() ����e���ܵ���
����e���ܵ���![]() ��
��
����![]() �քe��
�քe��![]() ��ƽ��
��ƽ��![]() �cƽ��
�cƽ��![]() ����ͶӰ����e���t�����c(di��n)
����ͶӰ����e���t�����c(di��n)![]() ��ʹ��
��ʹ��![]()
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com