
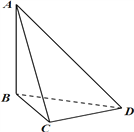
【題目】在三棱錐![]() 中,
中, ![]() 和
和![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 分別是
分別是![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析(2)見解析(3)![]() .
.
【解析】試題分析:(1)欲證OD∥平面PAC,根據直線與平面平行的判定定理可知只需證OD與平面PAC內一直線平行,而OD∥PA,PA平面PAC,OD平面PAC,滿足定理條件; (2)欲證平面PAB⊥平面ABC,根據面面垂直的判定定理可知在平面PAB內一直線與平面ABC垂直,而根據題意可得PO⊥平面ABC;
(3)根據OP垂直平面ABC得到OP為三棱錐P-ABC的高,根據三棱錐的體積公式可求出三棱錐P-ABC的體積.又因為D為PB中點,所以高是PO的一半.
試題解析:(1)∵![]() 分別為
分別為![]() 的中點,
的中點,
∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)連接![]() ,∵
,∵![]() 為
為![]() 中點,
中點, ![]() ,
,
∴![]() .
.
同理, ![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .
.
(3)由(2)可知![]() 平面
平面![]() ,
,
∴![]() 為三棱錐
為三棱錐![]() 的高,且
的高,且![]() .
.
∴![]() .
.


 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】圓C:(x﹣1)2+(y﹣2)2=25,直線l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)證明:不論m取什么數,直線l與圓C恒交于兩點;
(2)求直線l被圓C截得的線段的最短長度,并求此時m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一位網民在網上光顧某網店,經過一番瀏覽后,對該店鋪中的A,B,C三種商品有購買意向.已知該網民購買A種商品的概率為 ![]() ,購買B種商品的槪率為
,購買B種商品的槪率為 ![]() ,購買C種商品的概率為
,購買C種商品的概率為 ![]() .假設該網民是否購買這三種商品相互獨立
.假設該網民是否購買這三種商品相互獨立
(1)求該網民至少購買2種商品的概率;
(2)用隨機變量η表示該網民購買商品的種數,求η的槪率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足an+1=a ![]() ﹣nan+1,且a1=2.
﹣nan+1,且a1=2.
(1)計算a2 , a3 , a4的值,由此猜想數列{an}的通項公式,并用數學歸納法證明;
(2)求證:2nn≤a ![]() <3nn .
<3nn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】劉徽(約公元 225 年—295 年)是魏晉時期偉大的數學家,中國古典數學理論的奠基人之一,他的杰作《九章算術注》和《海島算經》是中國寶貴的古代數學遺產. 《九章算術·商功》中有這樣一段話:“斜解立方,得兩壍堵. 斜解壍堵,其一為陽馬,一為鱉臑.” 劉徽注:“此術臑者,背節也,或曰半陽馬,其形有似鱉肘,故以名云.” 其實這里所謂的“鱉臑(biē nào)”,就是在對長方體進行分割時所產生的四個面都為直角三角形的三棱錐. 如圖,在三棱錐![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,則三棱錐
,則三棱錐![]() 的外接球的球面面積為__________.
的外接球的球面面積為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 的圖象過點(﹣1,2),且在點(﹣1,f(﹣1))處的切線與直線x﹣5y+1=0垂直.
的圖象過點(﹣1,2),且在點(﹣1,f(﹣1))處的切線與直線x﹣5y+1=0垂直.
(1)求實數b,c的值;
(2)求f(x)在[﹣1,e](e為自然對數的底數)上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,a≠1且loga3>loga2,若函數f(x)=logax在區間[a,2a]上的最大值與最小值之差為1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函數g(x)=|logax﹣1|的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A1B1C1D1中,M、N分別為棱C1D1、C1C的中點,有以下四個結論: ①直線AM與CC1是相交直線;
②直線AM與BN是平行直線;
③直線BN與MB1是異面直線;
④直線AM與DD1是異面直線.
其中正確的結論為(注:把你認為正確的結論的序號都填上).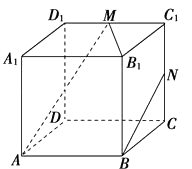
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com