
 .
.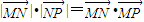 ,得
,得 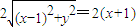 ,由此化簡能求出點P的軌跡C的方程.
,由此化簡能求出點P的軌跡C的方程.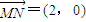 ,
,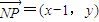 ,
,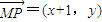 .(2分)
.(2分)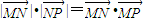 ,
,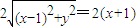 ,(4分)
,(4分)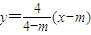 ,即4x+(m-4)y-4m=0,(8分)
,即4x+(m-4)y-4m=0,(8分)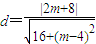 ,
, ,解得m<1;
,解得m<1;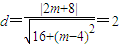 ,解得m=1;
,解得m=1;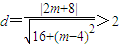 ,解得m>1.
,解得m>1.

 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
| MP |
| MN |
| PM |
| PN |
| NM |
| NP |
| PM |
| PN |
查看答案和解析>>
科目:高中數學 來源: 題型:
| PM |
| PN |
| A、(-∞,-5]∪[5,+∞) |
| B、(-∞,-25]∪[25,+∞) |
| C、[-25,25] |
| D、[-5,5] |
查看答案和解析>>
科目:高中數學 來源: 題型:
| MP |
| MN |
| PM |
| PN |
| NM |
| NP |
查看答案和解析>>
科目:高中數學 來源: 題型:
| MN |
| NP |
| MN |
| MP |
| FP1 |
| FP2 |
| 1 | ||
|
| 1 | ||
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| MN |
| NP |
| MN |
| MP |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com