
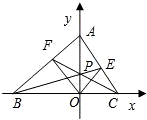
 如圖,在平面直角坐標系xoy中,設三角形ABC的頂點分別為A(0,a),B(b,0),C(c,0),點P(0,p)在線段AO上的一點(異于端點),這里a,b,c,p均為非零實數,設直線BP,CP分別與邊AC,AB交于點E,F.
如圖,在平面直角坐標系xoy中,設三角形ABC的頂點分別為A(0,a),B(b,0),C(c,0),點P(0,p)在線段AO上的一點(異于端點),這里a,b,c,p均為非零實數,設直線BP,CP分別與邊AC,AB交于點E,F.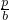 ,
, ,
,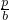 )(-
)(- )=-1,即pa=-bc;
)=-1,即pa=-bc;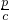 ,由A(0,a)和B(b,0)斜率為-
,由A(0,a)和B(b,0)斜率為- ,
,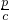 )(-
)(- )=
)=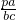 =
=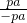 =-1,所以CF⊥AB;
=-1,所以CF⊥AB; |AC|,
|AC|, |AB|,所以F為線段AB的中點.
|AB|,所以F為線段AB的中點.

科目:高中數學 來源: 題型:
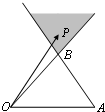 如圖,在△OAB中,點P是線段OB及線段AB延長線所圍成的陰影區域(含邊界)的任意一點,且
如圖,在△OAB中,點P是線段OB及線段AB延長線所圍成的陰影區域(含邊界)的任意一點,且| OP |
| OA |
| OB |
查看答案和解析>>
科目:高中數學 來源: 題型:
 1、如圖,在直角坐標平面內有一個邊長為a,中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數)與正六邊形交于M、N兩點,記△OMN的面積為S,則函數S=f(t)的奇偶性為
1、如圖,在直角坐標平面內有一個邊長為a,中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數)與正六邊形交于M、N兩點,記△OMN的面積為S,則函數S=f(t)的奇偶性為
查看答案和解析>>
科目:高中數學 來源: 題型:
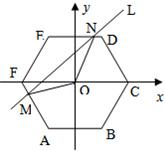 如圖,在直角坐標平面內有一個邊長為a、中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數)與正六邊形交于M、N兩點,記△OMN的面積為S,則函數S=f(t)的奇偶性為( )
如圖,在直角坐標平面內有一個邊長為a、中心在原點O的正六邊形ABCDEF,AB∥Ox.直線L:y=kx+t(k為常數)與正六邊形交于M、N兩點,記△OMN的面積為S,則函數S=f(t)的奇偶性為( )| A、偶函數 | B、奇函數 | C、不是奇函數,也不是偶函數 | D、奇偶性與k有關 |
查看答案和解析>>
科目:高中數學 來源: 題型:

試問:是否存在定點E、F,使|ME|、|MB|、|MF|成等差數列?若存在,求出E、F的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com