
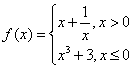 ,則方程
,則方程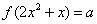 (
(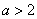 )的根的個數不可能為( )
)的根的個數不可能為( ) 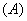 6
6  5
5  4
4  3
3 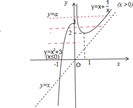
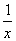 ≥2,當x≤0時,f(x)=x3+3≤3.于是可得:①當2<a<3時,f(x)=a有3個根,一負二正;②當a=3時,f(x)=a有3個根,一零二正;③當3<a時,f(x)=a有2個正根;④當a=2時,f(x)=a有一正一負根;⑤當a<2時,f(x)=a只有一負根.(2)令t=2x2+x=2(x+
≥2,當x≤0時,f(x)=x3+3≤3.于是可得:①當2<a<3時,f(x)=a有3個根,一負二正;②當a=3時,f(x)=a有3個根,一零二正;③當3<a時,f(x)=a有2個正根;④當a=2時,f(x)=a有一正一負根;⑤當a<2時,f(x)=a只有一負根.(2)令t=2x2+x=2(x+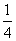 )2-
)2-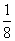
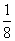 ,①當2<a<3時,f(t)=a有3個t使之成立,一負二正,兩個正t分別對應2個x,當t<-
,①當2<a<3時,f(t)=a有3個t使之成立,一負二正,兩個正t分別對應2個x,當t<-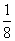 時,沒有x與之對應,當t=-
時,沒有x與之對應,當t=-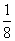 時,有1個x與之對應,當t>-
時,有1個x與之對應,當t>-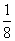 時,有2個x與之對應,∴根的個數分別為4、5、6個;②當3<a時,f(t)=a有2個正根,兩個正t分別對應2個x,此時根的個數為4個.③由題目不必考慮a≤2的情形.所以根的個數只可能為4、5、6個.即方程f(2x2+x)=a的根的個數只可能為4、5、6個,不可能為3個.故選A.
時,有2個x與之對應,∴根的個數分別為4、5、6個;②當3<a時,f(t)=a有2個正根,兩個正t分別對應2個x,此時根的個數為4個.③由題目不必考慮a≤2的情形.所以根的個數只可能為4、5、6個.即方程f(2x2+x)=a的根的個數只可能為4、5、6個,不可能為3個.故選A.

 輕松暑假總復習系列答案
輕松暑假總復習系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com