
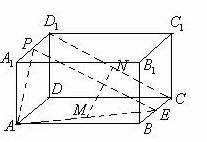
 如圖,長方體
如圖,長方體![]() 中,E、P分別是BC、
中,E、P分別是BC、![]() 的中點, M、N分別是AE、
的中點, M、N分別是AE、![]() 的中點,
的中點,![]() ,AB=2a
,AB=2a
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱錐![]() 的體積。
的體積。
解法一:(Ⅰ)證明:取CD的中點K,連結MK,NK
∵M,N,K分別為AK,CD1,CD的中點
∵MK//AD,NK//DD1
∴MK//面ADD1A1,NK//面ADD1A1
∴面MNK//面ADD1A1 ∴MN//面ADD1A1
(Ⅱ)設F為AD的中點
∵P為A1D1的中點 ∴PF//D1D ∴PF⊥面ABCD
作PH⊥AE,交AE于H,連結PH,則由三垂線定理得AE⊥PH
從而∠PHF為二面角P-AE-D的平面角。
在Rt△AEF中,AF=![]() ,EF=
,EF=![]() ,
,![]() ,
,
從而
在Rt△PFH中,![]()
故:二面角P-AE-D的大小為![]()
(Ⅲ)S△NEP=![]() =
=![]()
作DQ⊥CD1,交![]() 于Q,由A1D1⊥面 CDD1C1得 A1C1⊥DQ
于Q,由A1D1⊥面 CDD1C1得 A1C1⊥DQ
∴DQ⊥面BCD1A1
∴在Rt△CDD1中,![]()
∴VP-DEN=VD-ENP=![]() S△NEP?DQ=
S△NEP?DQ=![]()
解法二:以D為原點,DA,DC,DD1所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立直角坐標系,則
軸,建立直角坐標系,則
A(a,0,0), B(a,2a,0), C(0,2a,0), A1 (a,0,a), D1(0,.0,a)
∵E,P,M,N分別是BC,A1D1,AE,CD1的中點
∴![]()
(Ⅰ)![]()
取![]() ,顯然
,顯然![]()
![]() ,∴
,∴![]()
又![]() ∴
∴![]()
(Ⅱ)過P作PH⊥AE,交AE于H,取AD的中點F,則![]()
設![]() ,則
,則![]()
![]()
又![]()
由![]() ,及H在直線AE上,可得:
,及H在直線AE上,可得: 
解得![]()
∴![]()
![]()
∴![]() 即
即![]()
∴![]() 與
與![]() 所夾的角等于二面角P-AE-D的大小
所夾的角等于二面角P-AE-D的大小

故:二面角P-AE-D的大小為![]()
(Ⅲ)設![]() 為平面DEN的法向量,則
為平面DEN的法向量,則![]() ,
,![]()
又![]() ,
,![]() ,
,![]()
∴ 即
即 ∴可取
∴可取![]()
∴P點到平面DEN的距離為
∵ ,
,
![]()
∴![]()
∴![]()


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:
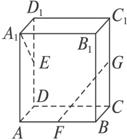
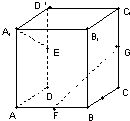 如圖長方體ABCD-A1B1C1D1中,AA1=AB=4,AD=2,E、F、G分別是DD1、AB、CC1的中點,則直線A1E,FG所夾的角的余弦值為
如圖長方體ABCD-A1B1C1D1中,AA1=AB=4,AD=2,E、F、G分別是DD1、AB、CC1的中點,則直線A1E,FG所夾的角的余弦值為查看答案和解析>>
科目:高中數學 來源: 題型:
(06年四川卷理)(12分)
如圖,長方體ABCD-![]() 中,E、P分別是BC、
中,E、P分別是BC、![]() 的中點,
的中點,
M、N分別是AE、![]() 的中點,
的中點, ![]()
![]()
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱錐P-DEN的體積。

查看答案和解析>>
科目:高中數學 來源: 題型:
A.arccos![]() B.
B.![]()
C.arccos![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:

A.arccos![]() B.
B.![]()
C.arccos![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com