
| x-3 |
| x+3 |
| 1 |
| 2 |
| x-3 |
| x+3 |
| x-3 |
| x+3 |
| -x-3 |
| -x+3 |
| (x-3)(-x-3) |
| (3+x)(3-x) |
| 1 |
| 2 |
| x-3 |
| x+3 |
| 1 |
| 2 |
| -6 |
| x+3 |
| x-3 |
| x+3 |
| x-3 |
| x+3 |
| -x-3 |
| -x+3 |
| (x-3)(-x-3) |
| (3+x)(3-x) |
| 1 |
| 2 |
| 1 |
| 2 |
| x-3 |
| x+3 |
| 1 |
| 2 |
| -6 |
| x+3 |
| -6 |
| x +3 |
| 1 |
| 2 |
| 1 |
| 2 |
| x-3 |
| x+3 |
| 1 |
| 2 |
| -6 |
| x+3 |


科目:高中數學 來源: 題型:解答題
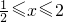 }且M∩P≠∅求實數a的取值范圍;
}且M∩P≠∅求實數a的取值范圍;查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市東城區東直門中學高三數學提高測試試卷7(理科)(解析版) 題型:解答題
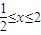 }且M∩P≠∅求實數a的取值范圍;
}且M∩P≠∅求實數a的取值范圍;查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省揚州中學高三(下)開學檢測數學試卷(解析版) 題型:解答題
 在(0,+∞)上為增函數,則稱f(x)為“一階比增函數”;若y=
在(0,+∞)上為增函數,則稱f(x)為“一階比增函數”;若y= 在(0,+∞)上為增函數,則稱f(x)為“二階比增函數”.我們把所有“一階比增函數”組成的集合記為Ω1,所有“二階比增函數”組成的集合記為Ω2.
在(0,+∞)上為增函數,則稱f(x)為“二階比增函數”.我們把所有“一階比增函數”組成的集合記為Ω1,所有“二階比增函數”組成的集合記為Ω2.| x | a | b | c | a+b+c |
| f(x) | d | d | t | 4 |
查看答案和解析>>
科目:高中數學 來源:2011-2012年江西省貴溪一中等五校高三(下)第一次聯考數學試卷(理科)(解析版) 題型:解答題
 }且M∩P≠∅求實數a的取值范圍;
}且M∩P≠∅求實數a的取值范圍;查看答案和解析>>
科目:高中數學 來源:2011年福建省泉州市安溪八中高考數學模擬試卷(理科)(解析版) 題型:解答題
 }且M∩P≠∅求實數a的取值范圍;
}且M∩P≠∅求實數a的取值范圍;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com