【答案】
分析:(1)利用函數極值的定義得出數列相鄰兩項之間的關系是解決本題的關鍵,關鍵要確定出相關數列為特殊數列,從而達到求解的目的;
(2)求出數列{b
n}的前n項和S
n是解決本題的關鍵,根據已知條件確定出關于n的不等式,通過解不等式求出正整數n的最小值;
(3)首先要確定出c
n的表達式,利用分析法完成不等式的證明,注意約分思想的運用.
解答:解:(1)f′(x)=3a
n-1x
2-3[(t+1)a
n-a
n+1],
所以
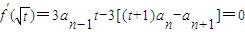
.整理得:a
n+1-a
n=t(a
n-a
n-1).
當t=1時,{a
n-a
n-1}是常數列,得a
n=1;
當t≠1時,{a
n-a
n-1}是以a
2-a
1=t
2-t為首項,t為公比的等比數列,所以a
n-a
n-1=(t
2-t)•t
n-2=(t-1)•t
n-1由上式得:a
n-t
n=a
n-1-t
n-1,所以{a
n-t
n}是常數列,a
n-t
n=a
1-t=0,a
n=t
n(n≥2).又,當t=1時上式仍然成立,故a
n=t
n(n∈N
*).
(2)當t=2時,
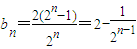
∴
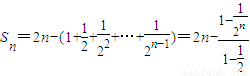
=
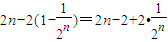
.
由S
n>2010,得
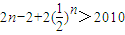
,

,
當

,
因此n的最小值為1006.
(3)
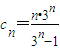
且

,所以

等價于
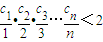
等價于
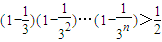
因為
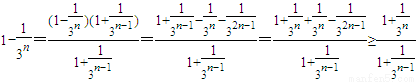
,
所以
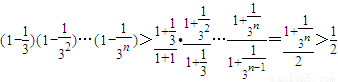
,從而原命題得證.
點評:本題屬于函數、數列、不等式的綜合問題,首先通過數列與函數的聯系,得出數列某些項之間的關系,然后利用數列的知識實現求通項和求前n項和的計算,考查分析法證明不等式的思想和意識.

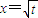 是函數f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一個極值點.數列{an}中a1=t,a2=t2(t>0且t≠1).
是函數f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一個極值點.數列{an}中a1=t,a2=t2(t>0且t≠1).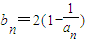 ,當t=2時,數列{bn}的前n項和為Sn,求使Sn>2010的n的最小值;
,當t=2時,數列{bn}的前n項和為Sn,求使Sn>2010的n的最小值;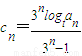 ,證明:
,證明: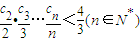 .
.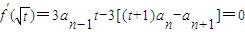 .整理得:an+1-an=t(an-an-1).
.整理得:an+1-an=t(an-an-1).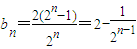 ∴
∴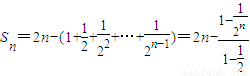
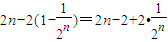 .
.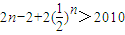 ,
, ,
, ,
,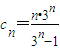 且
且 ,所以
,所以 等價于
等價于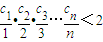 等價于
等價于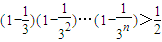
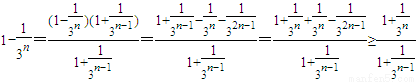 ,
,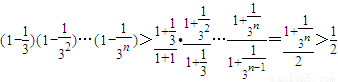 ,從而原命題得證.
,從而原命題得證.

 輕松暑假總復習系列答案
輕松暑假總復習系列答案