【答案】
分析:(1)對函數f(x)求導,再令自變量為1,求出f′(1)得到函數的解析式及導數,再由導數求函數的單調區間;
(2)由題意
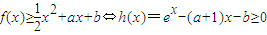
,借助導數求出新函數的最小值,令其大于0即可得到參數a,b 所滿足的關系式,再研究(a+1)b的最大值
解答:解:(1)
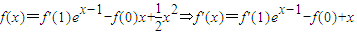
令x=1得:f(0)=1
∴
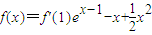
令x=0,得f(0)=f'(1)e
-1=1解得f'(1)=e
故函數的解析式為
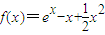
令g(x)=f'(x)=e
x-1+x
∴g'(x)=e
x+1>0,由此知y=g(x)在x∈R上單調遞增
當x>0時,f'(x)>f'(0)=0;當x<0時,有
f'(x)<f'(0)=0得:
函數
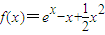
的單調遞增區間為(0,+∞),單調遞減區間為(-∞,0)
(2)
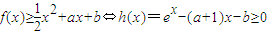
得h′(x)=e
x-(a+1)
①當a+1≤0時,h′(x)>0⇒y=h(x)在x∈R上單調遞增x→-∞時,h(x)→-∞與h(x)≥0矛盾
②當a+1>0時,h′(x)>0?x>ln(a+1),h'(x)<0?x<ln(a+1)
得:當x=ln(a+1)時,h(x)
min=(a+1)-(a+1)ln(a+1)-b≥0,即(a+1)-(a+1)ln(a+1)≥b
∴(a+1)b≤(a+1)
2-(a+1)
2ln(a+1),(a+1>0)
令F(x)=x
2-x
2lnx(x>0),則F'(x)=x(1-2lnx)
∴
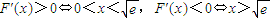
當
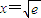
時,
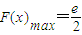
即當
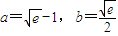
時,(a+1)b的最大值為
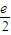 點評:
點評:本題考查導數在最值問題中的應用及利用導數研究函數的單調性,解題的關鍵是第一題中要賦值求出f′(1),易因為沒有將f′(1)看作常數而出錯,第二題中將不等式恒成立研究參數關系的問題轉化為最小值問題,本題考查了轉化的思想,考查判斷推理能力,是高考中的熱點題型,難度較大,計算量也大,易馬虎出錯

 ;
;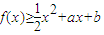 ,求(a+1)b的最大值.
,求(a+1)b的最大值.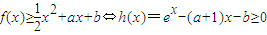 ,借助導數求出新函數的最小值,令其大于0即可得到參數a,b 所滿足的關系式,再研究(a+1)b的最大值
,借助導數求出新函數的最小值,令其大于0即可得到參數a,b 所滿足的關系式,再研究(a+1)b的最大值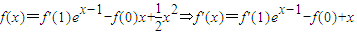
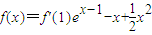 令x=0,得f(0)=f'(1)e-1=1解得f'(1)=e
令x=0,得f(0)=f'(1)e-1=1解得f'(1)=e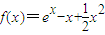
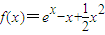 的單調遞增區間為(0,+∞),單調遞減區間為(-∞,0)
的單調遞增區間為(0,+∞),單調遞減區間為(-∞,0)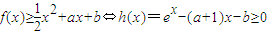 得h′(x)=ex-(a+1)
得h′(x)=ex-(a+1)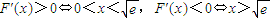
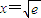 時,
時,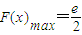
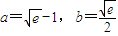 時,(a+1)b的最大值為
時,(a+1)b的最大值為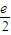


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案