
���}Ŀ����֪�E�A![]() ���x���ʞ�
���x���ʞ�![]() ���ҽ��c(di��n)��A
���ҽ��c(di��n)��A![]() �ĈA�ģ��҈A
�ĈA�ģ��҈A![]() ��
��![]() �S�������L(zh��ng)��4��
�S�������L(zh��ng)��4��
��1����E�A![]() �c�A
�c�A![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() �c����
�c����![]() ��
��![]() ��ֻ��һ��(g��)�����c(di��n)��ӛֱ��
��ֻ��һ��(g��)�����c(di��n)��ӛֱ��![]() �c�A
�c�A![]() �����c(di��n)��
�����c(di��n)��![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��
���𰸡�(1) �E�A![]() �ķ��̞�
�ķ��̞�![]() ���A
���A![]() �ķ��̞�
�ķ��̞�![]() �� (2)
�� (2) ![]() ��
��![]() ��
��
��������
��1���əE�A���x���ʞ�![]() ���ҽ��c(di��n)��AC2����x��1��2+y2��r2�ĈA�ģ��г����̽M�����a��b��c���ɴ�������E�A
���ҽ��c(di��n)��AC2����x��1��2+y2��r2�ĈA�ģ��г����̽M�����a��b��c���ɴ�������E�A![]() �ķ��̣��ɈA
�ķ��̣��ɈA![]() ��y�S�������L(zh��ng)��4����
��y�S�������L(zh��ng)��4����![]() ��22+12��5���ɴ�������A
��22+12��5���ɴ�������A![]() �ķ��̣���2���O(sh��)ֱ��l�ķ��̞�y��kx+m���ƌ�(d��o)��4k2��m2��2km��5����
�ķ��̣���2���O(sh��)ֱ��l�ķ��̞�y��kx+m���ƌ�(d��o)��4k2��m2��2km��5����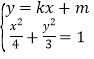 ���ã�3+4k2��x2+8kmx+4m2��12��0���ɴ����ø����Єeʽ��ֱ�����̡��A���E�A���|(zh��)���Y(ji��)����֪�l�������ֱ��l�c�A
���ã�3+4k2��x2+8kmx+4m2��12��0���ɴ����ø����Єeʽ��ֱ�����̡��A���E�A���|(zh��)���Y(ji��)����֪�l�������ֱ��l�c�A![]() �Ĺ����c(di��n)A������(bi��o)��
�����c(di��n)A������(bi��o)��
��1�����}��֪��![]() ���
���![]()
��![]() ��
��
���ԙE�A![]() �ķ��̞�
�ķ��̞�![]() ��
��
��?y��n)�A![]() ��
��![]() �S�������L(zh��ng)��4������
�S�������L(zh��ng)��4������![]() ��
��
���ԈA![]() �ķ��̞�
�ķ��̞�![]() ��
��
��2���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ���t
���t
![]() ��
��
��![]() ��
��
�� ��
��![]() ��
��
��?y��n)�ֱ��![]() �c����
�c����![]() ֻ��һ��(g��)�����c(di��n)������
ֻ��һ��(g��)�����c(di��n)������
![]() ��
��
����(ji��n)���� ![]() ��
��
�٢�(li��n)������� ��
��
��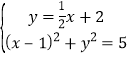 ���
���![]() ��
��
��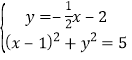 ���
���![]() ��
��
��ֱ��![]() �c�A
�c�A![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��
��![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
��1����(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ǡ�Ѓɂ�(g��)��ͬ�����c(di��n)����(sh��)��(sh��)
ǡ�Ѓɂ�(g��)��ͬ�����c(di��n)����(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2����(d��ng)![]() �r(sh��)��
�r(sh��)��
�� ��(du��)������![]() ������
������![]() ����
����![]() ��ȡֵ������
��ȡֵ������
�� ��![]() ����(sh��)
����(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ����ֵ
�ϵ����ֵ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���h��ʮ�˴��ԁ�(l��i),�҇�(gu��)����(zh��n)��ؚ�ѽ�(j��ng)��(sh��)ʩ������,�҇�(gu��)ؚ���˿ڏ�2012���9899�f(w��n)��,�p�ٵ�2018���1660�f(w��n)��,2019�ꌢŬ����(sh��)�F(xi��n)�p��ؚ���˿�1000�f(w��n)�����ϵ�Ŀ��(bi��o),����(zh��ng)2020���ڬF(xi��n)�И�(bi��o)��(zh��n)��,�r(n��ng)��ؚ���˿�ȫ��Óؚ,ؚ���hȫ��Óؚժñ.ij�О��������ԓ�Ю�(d��ng)ǰ��ؚ�I(l��ng)����ڵ�ͻ�����},�з�ؚ�k�������(l��i),ÿ���ꌦ(du��)ؚ����(��![]() ��ʾ,��λ:�f(w��n)��)�M(j��n)��ȡ��,�y(t��ng)Ӌ(j��)�Y(ji��)����D��ʾ,��2016��6�µ�2019��6�µĹ��M(j��n)�����ߴνy(t��ng)Ӌ(j��),�y(t��ng)Ӌ(j��)�r(sh��)�g����̖(h��o)
��ʾ,��λ:�f(w��n)��)�M(j��n)��ȡ��,�y(t��ng)Ӌ(j��)�Y(ji��)����D��ʾ,��2016��6�µ�2019��6�µĹ��M(j��n)�����ߴνy(t��ng)Ӌ(j��),�y(t��ng)Ӌ(j��)�r(sh��)�g����̖(h��o)![]() ��ʾ,����:2016��12�µ�(�r(sh��)�g��̖(h��o)��2)ؚ������5.2�f(w��n)��.
��ʾ,����:2016��12�µ�(�r(sh��)�g��̖(h��o)��2)ؚ������5.2�f(w��n)��.

(1)��![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw����
�ľ��Իؚw����![]() ,���A(y��)�y(c��)��2020��12�µ�,ԓ���ܷ�(sh��)�F(xi��n)ؚ����ȫ��Óؚ;
,���A(y��)�y(c��)��2020��12�µ�,ԓ���ܷ�(sh��)�F(xi��n)ؚ����ȫ��Óؚ;
(2)��M����AÓؚ����(ji��n)��(zh��n),ԓ�з�ؚ�k��2019��6�µוr(sh��),��(du��)ȫ��ؚ�����S�C(j��)��ȡ��100��ؚ����,��(du��)ÿ��(g��)��ͥ����Ҫ��(j��ng)��(j��)�����(l��i)Դ�M(j��n)�г���{(di��o)��,�y(t��ng)Ӌ(j��)�Y(ji��)����D.���Q����(j��)���x��һ���r(n��ng)�I(y��)���g(sh��)�ˆT��(du��)ȫ������ؚ������,��ͥ����Ҫ��(j��ng)��(j��)�����(l��i)Դ���B(y��ng)ֳ����ͷNֲ�����ؚ�����M(j��n)�Ќ�(du��)�ڎͷ�,ÿһ���r(n��ng)�I(y��)���g(sh��)�ˆT��(du��)�ڎͷ�ؚ����90��,�tԓ�Б�(y��ng)�քe���Ŷ����r(n��ng)�I(y��)���g(sh��)�ˆT��(du��)��ͥ����Ҫ��(j��ng)��(j��)�����(l��i)Դ���B(y��ng)ֳ����ͷNֲ�����ؚ�����M(j��n)�Ќ�(du��)�ڎͷ�?
��:�ؚwֱ����б�ʺͽؾ����С���˷���Ӌ(j��)��ʽ�քe��:
 ,
,![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����C�ĘO����(bi��o)���̞���2��![]() .
.
(1)���ԘO�c(di��n)��ƽ��ֱ������(bi��o)ϵ��ԭ�c(di��n)���O�S��x�S�������S������ƽ��ֱ������(bi��o)ϵ��������C��ֱ������(bi��o)���̣�
(2)��P(x��y)������C�ϵ�һ��(g��)��(d��ng)�c(di��n)����3x��4y�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���タ![]()
![]() ���^ֱ��
���^ֱ��![]() ��
��![]() ����һ�c(di��n)
����һ�c(di��n)![]() ���タ
���タ![]() ���ɗl�о�
���ɗl�о�![]() �����c(di��n)��
�����c(di��n)��![]() �����c(di��n)
�����c(di��n)![]() ��
��![]() �S�Ϸ�����
�S�Ϸ�����
��1�����C��ֱ��![]() �^���c(di��n)�������ԓ���c(di��n)��
�^���c(di��n)�������ԓ���c(di��n)��
��2�����タ![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M��12�֣�
��D�������F![]() �ĵ���
�ĵ���![]() �����Σ�
�����Σ�![]() ƽ��
ƽ��![]() ��
��![]() ��
��
![]() �քe��
�քe��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��

���������C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��������ƽ��![]() �cƽ��
�cƽ��![]() ���ɵ��J����ǵ�����ֵ��
���ɵ��J����ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������(sh��)
������(sh��)![]() �Dž^(q��)�g
�Dž^(q��)�g![]() �ϵĜp����(sh��).
�ϵĜp����(sh��).
��1����![]() �����ֵ��
�����ֵ��
��2����![]() ��
��![]() �Ϻ��������
�Ϻ��������![]() ��ȡֵ������
��ȡֵ������
��3��ӑՓ�P(gu��n)��![]() �ķ���
�ķ���![]() �ĸ��Ă�(g��)��(sh��).
�ĸ��Ă�(g��)��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���P(gu��n)�ں���(sh��)![]() �������Ă�(g��)�Y(ji��)Փ������
�������Ă�(g��)�Y(ji��)Փ������![]() ���t
���t![]() ����
����![]() �ĈD���P(gu��n)���c(di��n)
�ĈD���P(gu��n)���c(di��n)![]() ��(du��)�Q���ۺ���(sh��)
��(du��)�Q���ۺ���(sh��)![]() ��
��![]() �φ��{(di��o)�f������
�φ��{(di��o)�f������![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ��(g��)��λ�L(zh��ng)�Ⱥ����ÈD���P(gu��n)��
��(g��)��λ�L(zh��ng)�Ⱥ����ÈD���P(gu��n)��![]() �S��(du��)�Q.�����������_�Y(ji��)Փ�ľ�̖(h��o)�ǣ� ��
�S��(du��)�Q.�����������_�Y(ji��)Փ�ľ�̖(h��o)�ǣ� ��
A.�٢ڢ�B.�٢�C.�ۢ�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���R��(hu��)���҇�(gu��)���ϵĂ��y(t��ng)�����Ļ����(d��ng),�ַQ���R�С��� ����(ji��)��(ch��ng)��.�R��(hu��)����ڴ���(ji��)��Ԫ����(ji��)�ȹ�(ji��)���e��.�R��(hu��)�����S����ʵ��Ļ��ʘ����(d��ng),�硰�ҽ���������ÿ������һ�w��,����Ъ�(ji��ng)Ʒ,�t���Ъ�(ji��ng)����.���괺��(ji��)���g,ijУ�ס��ҡ���������λͬ�W(xu��)��s��(l��i)��ij�R��(hu��),ÿ�˾��@����һ�w�ęC(j��)��(hu��).�Α��_ʼǰ,�ס��ҡ���������λͬ�W(xu��)��(du��)�Α��Ъ�(ji��ng)�Y(ji��)���M(j��n)�����A(y��)�y(c��),�A(y��)�y(c��)�Y(ji��)������:
���f(shu��):���һ������Ъ�(ji��ng)���� ���f(shu��):�������Ъ�(ji��ng)����
���f(shu��):���һ������Ъ�(ji��ng)���� ���f(shu��):���ײ����Ъ�(ji��ng)��.
�Α�Y(ji��)����,�@��λͬ�W(xu��)��ֻ��һλͬ�W(xu��)�Ъ�(ji��ng),��ֻ��һλͬ�W(xu��)���A(y��)�y(c��)�Y(ji��)�������_��,�t�Ъ�(ji��ng)��ͬ�W(xu��)��( )

A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com