
某住宅小區計劃植樹不少于100棵,若第一天植2棵,以后每天植樹的棵樹是前一天的2倍,則需要的最少天數n(n∈N*)為________.
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第八章第3課時練習卷(解析版) 題型:填空題
P為△ABC所在平面外一點,O為P在平面ABC內的射影.
(1)若P到△ABC三邊距離相等,且O在△ABC的內部,則O是△ABC的________心;
(2)若PA⊥BC,PB⊥AC,則O是△ABC的________心;
(3)若PA,PB,PC與底面所成的角相等,則O是△ABC的________心.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第6課時練習卷(解析版) 題型:解答題
已知數列{an}滿足a1+a2+…+an=n2(n∈N*).
(1)求數列{an}的通項公式;
(2)對任意給定的k∈N*,是否存在p,r∈N*(k<p<r)使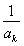 ,
,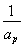 ,
,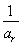 成等差數列?若存在,用k分別表示p和r(只要寫出一組);若不存在,請說明理由.
成等差數列?若存在,用k分別表示p和r(只要寫出一組);若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第5課時練習卷(解析版) 題型:解答題
我國是一個人口大國,隨著時間推移,老齡化現象越來越嚴重,為緩解社會和家庭壓力,決定采用養老儲備金制度.公民在就業的第一年交納養老儲備金,數目為a1,以后每年交納的數目均比上一年增加d(d>0),因此,歷年所交納的儲備金數目a1,a2,…,an是一個公差為d的等差數列.與此同時,國家給予優惠的計息政策,不僅采用固定利率,而且計算復利.這就是說,如果固定利率為r(r>0),那么,在第n年末,第一年所交納的儲備金就變為a1(1+r)n-1,第二年所交納的儲備金就變為a2(1+r)n-2,…,以Tn表示到第n年所累計的儲備金總額.
(1)寫出Tn與Tn-1(n≥2)的遞推關系式;
(2)求證:Tn=An+Bn,其中{An}是一個等比數列,{Bn}是一個等差數列.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第5課時練習卷(解析版) 題型:解答題
已知數列{an}是首項為1,公差為d的等差數列,數列{bn}是首項為1,公比為q(q>1)的等比數列.
(1)若a5=b5,q=3,求數列{an·bn}的前n項和;
(2)若存在正整數k(k≥2),使得ak=bk.試比較an與bn的大小,并說明理由..
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第4課時練習卷(解析版) 題型:解答題
已知數列an= 求a1+a2+a3+a4+…+a99+a100的值.
求a1+a2+a3+a4+…+a99+a100的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第3課時練習卷(解析版) 題型:填空題
定義在(-∞,0)∪(0,+∞)上的函數f(x),如果對于任意給定的等比數列{an},{f(an)}仍是等比數列,則稱f(x)為“保等比數列函數”.現有定義在(-∞,0)∪(0,+∞)上的如下函數:
①f(x)=x2;②f(x)=2x;③f(x)=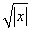 ;④f(x)=ln(x).
;④f(x)=ln(x).
其中是“保等比數列函數”的是__________.(填序號)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第1課時練習卷(解析版) 題型:解答題
如下表定義函數f(x):
x | 1 | 2 | 3 | 4 | 5 |
f(x) | 5 | 4 | 3 | 1 | 2 |
對于數列{an},a1=4,an=f(an-1),n=2,3,4,…,求a2008.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com