
【題目】在以ABCDEF為頂點的五面體中,底面ABCD為菱形,∠ABC=120°,AB=AE=ED=2EF,EF![]() AB,點G為CD中點,平面EAD⊥平面ABCD.
AB,點G為CD中點,平面EAD⊥平面ABCD.
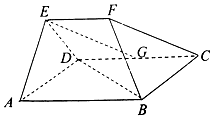
(1)證明:BD⊥EG;
(2)若三棱錐![]() ,求菱形ABCD的邊長.
,求菱形ABCD的邊長.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 的各項均為正整數(shù),Sn為其前n項和,對于n=1,2,3,…,有
的各項均為正整數(shù),Sn為其前n項和,對于n=1,2,3,…,有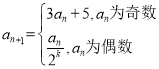 ,其中
,其中![]() 為使
為使![]() 為奇數(shù)的正整數(shù),當
為奇數(shù)的正整數(shù),當![]() 時,
時,![]() 的最小值為__________;當
的最小值為__________;當![]() 時,
時,![]() ___________.
___________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】交通部門調查在高速公路上的平均車速情況,隨機抽查了60名家庭轎車駕駛員,統(tǒng)計其中有40名男性駕駛員,其中平均車速超過![]() 的有30人,不超過
的有30人,不超過![]() 的有10人;在其余20名女性駕駛員中,平均車速超過
的有10人;在其余20名女性駕駛員中,平均車速超過![]() 的有5人,不超過
的有5人,不超過![]() 的有15人.
的有15人.
(1)完成下面的![]() 列聯(lián)表,并據(jù)此判斷是否有
列聯(lián)表,并據(jù)此判斷是否有![]() 的把握認為,家庭轎車平均車速超過
的把握認為,家庭轎車平均車速超過![]() 與駕駛員的性別有關;
與駕駛員的性別有關;
平均車速超過 | 平均車速不超過 | 合計 | |
男性駕駛員 | |||
女性駕駛員 | |||
合計 |
(2)根據(jù)這些樣本數(shù)據(jù)來估計總體,隨機調查3輛家庭轎車,記這3輛車中,駕駛員為女性且平均車速不超過![]() 的人數(shù)為
的人數(shù)為![]() ,假定抽取的結果相互獨立,求
,假定抽取的結果相互獨立,求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
參考公式: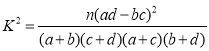
![]()
臨界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點N在曲線![]() 上,直線
上,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,動點
,動點![]() 滿足
滿足![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]()
(1)求![]() 的軌跡方程;
的軌跡方程;
(2)若過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 上 (
上 (![]() 為坐標原點),求證:
為坐標原點),求證:![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(12分)已知函數(shù)![]() .
.
(1)若x=2是函數(shù)f(x)的極值點,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若函數(shù)f(x)在![]() 上為單調增函數(shù),求a的取值范圍;
上為單調增函數(shù),求a的取值范圍;
(3)設m,n為正實數(shù),且m>n,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,左右焦點分別為
,左右焦點分別為![]() ,
,![]() ,點
,點![]() 是橢圓上位于第一象限的任一點,且當
是橢圓上位于第一象限的任一點,且當![]() 時,
時,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若橢圓![]() 上點
上點![]() 與點
與點![]() 關于原點
關于原點![]() 對稱,過點
對稱,過點![]() 作
作![]() 垂直于
垂直于![]() 軸,垂足為
軸,垂足為![]() ,連接
,連接![]() 并延長交
并延長交![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() .
.
(ⅰ)求![]() 面積最大值;
面積最大值;
(ⅱ)證明:直線![]() 與
與![]() 斜率之積為定值.
斜率之積為定值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com