
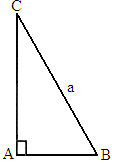
(19)如圖,在Rt△ABC中,已知BC=a,若長為2a的線段PQ以點A為中點,問![]() 與
與![]() 的夾角θ取何值時
的夾角θ取何值時
![]() ·
·![]() 的值最大?并求出這個最大值.
的值最大?并求出這個最大值.
(19)本小題主要考查向量的概念,平面向量的運算法則,考查運用向量及函數知識的能力.
解法一:∵![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =0.
=0.
∵![]() =-
=-![]() ,
,![]() =
=![]() -
-![]() ,
,![]() =
=![]() -
-![]() ,
,
∴![]() ·
·![]() =(
=(![]() -
-![]() )·(
)·(![]() -
-![]() )
)
=![]() ·
·![]() -
-![]() ·
·![]() -
-![]() ·
·![]() +
+![]() ·
·![]()
=-a2-![]() ·
·![]() +
+![]() ·
·![]()
=-a2+![]() ·(
·(![]() -
-![]() )
)
=-a2+![]()
![]() ·
·![]()
=-a2+a2cosθ.
故當cosθ=1,即θ=0(![]() 與
與![]() 方向相同)時,
方向相同)時,![]() ·
·![]() 最大,其最大值為0.
最大,其最大值為0.
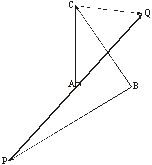
解法二:以直角頂點A為坐標原點,兩直角邊所在直線為坐標軸建立如圖所示的平面直角坐標系.

設|AB|=c,|AC|=b,則A(0,0),B(c,0),C(0,b).
且|PQ|=2a,|BC|=a.
設點P的坐標為(x,y),則Q(-x,-y).
∴![]() =(x-c,y),
=(x-c,y), ![]() =(-x,-y-b),
=(-x,-y-b), ![]() =(-c,b),
=(-c,b),![]() =(-2x,-2y).
=(-2x,-2y).
∴![]() ·
·![]() =(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.
=(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.
∵cosθ= =
=![]() ,
,
∴cx-by=a2cosθ.
∴![]() ·
·![]() =-a2+a2cosθ.
=-a2+a2cosθ.
故當cosθ=1,即θ=0(PQ與BC方向相同)時, ![]() ·
·![]() 最大,其最大值為0.
最大,其最大值為0.


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:044
(2004
湖北,19)如圖所示,在Rt△ABC中,已知BC=a,若長為2a的線段PQ以點A為中點,問 與
與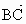 的夾角θ取何值時
的夾角θ取何值時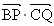 的值最大?并求出這個最大值.
的值最大?并求出這個最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com