【題目】已知函數
（1）求曲線
在點
處的切線方程;
（2）令
，討論
的單調性并判斷有無極值，若有，求出極值.
【答案】（1）y=1（2）見解析
【解析】試題分析：（1）求出函數
的導數，分別求出
， 
，即可求出曲線
在點
處的切線方程；（2）表示出
的表達式，求出
的導數，構造
，可證
時， 
； 
時， 
，再對
分類討論，根據導數，求出單調區間，并可判斷有無極值，從而求出極值.
試題解析：（1）
∴
則切線方程為
（2）依題意得
∴
令
，則
∴函數
在R上單調遞增．
∵
∴
時， 
； 
時， 
當
時， 
，則
時， 
，函數
在（0，+∞）單調遞增； 
時， 
，函數
在（﹣∞，0）單調遞減．
∴
時，函數
取得極小值， 
，無極大值
當
時，令
，則
， 
①
時， 
時， 
， 
，函數
單調遞增；
時， 
， 
，函數
單調遞減；
時， 
， 
，函數
單調遞增
∴當
時，函數
取得極小值， 
．當
時，函數
取得極大值， 
②
時， 
， 
時， 
∴函數
在
上單調遞增，無極值
③
時， 
， 
時， 
， 
，函數
單調遞增；
時， 
， 
，函數
單調遞減；
時， 
， 
，函數
單調遞增．
∴當
時，函數
取得極大值， 
，當
時，函數
取得極小值, 
綜上所述：當
時，函數
在（0，+∞）單調遞增，在（﹣∞，0）單調遞減， 
極小值為﹣1﹣2a，無極大值；
當
時，函數
在
，（0，+∞）上單調遞增，在
上單調遞減， 
極小值為
，極大值為
當
時，函數
在
上單調遞增，無極值
當
時，函數
在（﹣∞，0），
上單調遞增，在
上單調遞減， 
極大值為
．極小值為
．
科目：高中數學 來源： 題型：
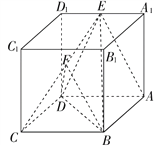
【題目】如圖，正方體ABCD－A1B1C1D1中，點E是A1D1的中點，點F是CE的中點．
(Ⅰ)求證：平面ACE⊥平面BDD1B1；
(Ⅱ)求證：AE∥平面BDF.
查看答案和解析>>
科目：高中數學 來源： 題型：
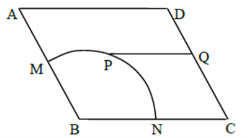
【題目】如圖，某廣場中間有一塊邊長為2百米的菱形狀綠化區
，其中
是半徑為1百米的扇形，
． 管理部門欲在該地從
到
修建小路：在弧
上選一點
（異于
兩點），過點
修建與
平行的小路
．問：點
選擇在何處時，才能使得修建的小路
與
及
的總長最小？并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856323)已知在△ABC中，A，B，C所對的邊分別為a，b，c，R為△ABC外接圓的半徑，若a＝1， 
sin2B＋
sin2C－sin2A＝sin Asin Bsin C，則R的值為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856335)[選修4－4：坐標系與參數方程]
以原點為極點，x軸的非負半軸為極軸建立極坐標系．已知A(2，π)，B(2， 
)，圓C的極坐標方程為ρ2－6ρcos θ＋8ρsin θ＋21＝0.F為圓C上的任意一點．
(Ⅰ)寫出圓C的參數方程；
(Ⅱ)求△ABF的面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】共享單車是指企業的校園，地鐵站點、公交站點、居民區、商業區、公共服務區等提供自行車單車共享服務，是一種分時租賃模式，某共享單車企業為更好服務社會，隨機調查了100人，統計了這100人每日平均騎行共享單車的時間（單位：分鐘），由統計數據得到如下頻率分布直方圖，已知騎行時間在
三組對應的人數依次成等差數列
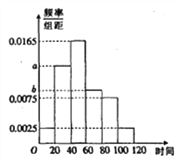
（1）求頻率分布直方圖中
的值.
（2）若將日平均騎行時間不少于80分鐘的用戶定義為“忠實用戶”，將日平均騎行時間少于40分鐘的用戶為“潛力用戶”，現從上述“忠實用戶”與“潛力用戶”的人中按分層抽樣選出5人，再從這5人中任取3人，求恰好1人為“忠實用戶”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝x2＋(x－1)|x－a|.
(1)若a＝－1，解方程f(x)＝1；
(2)若函數f(x)在R上單調遞增，求實數a的取值范圍；
(3)是否存在實數a，使不等式f(x)≥2x－3對任意x∈R恒成立？若存在，求出a的取值范圍；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體ABCD-A1B1C1D1的棱長為1，線段B1D1上有兩個動點E，F，且EF=
，則下列結論中錯誤的是( )
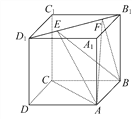
A. AC⊥BE
B. EF∥平面ABCD
C. 三棱錐A-BEF的體積為定值
D. △AEF的面積與△BEF的面積相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
