
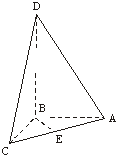
18.如圖所示四面體ABCD中,AB、BC、BD兩兩互相垂直,且AB=BC=2,E是AC中點,異面直線
AD與BE所成的角的大小為arccos![]() .求四面體ABCD的體積.
.求四面體ABCD的體積.
18.解法一:如圖建立空間直角坐標系.
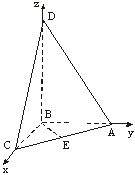
由題意,有A(0,2,0),C(2,0,0),E(1,1,0).
設D點的坐標為(0,0,z)(z>0),
則![]() ={1,1,0},
={1,1,0},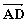 ={0,-2,z}.
={0,-2,z}.
設![]() 與
與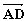 所成的角為
所成的角為![]() ,
,
則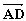 ·
·![]() =
=![]() =-2,
=-2,
且AD與BE所成的角的大小為![]() ,
,
∴![]() ,
,
得z=4,故BD的長度是4.
又VABCD=![]() ,
,
因此四面體ABCD的體積是![]() .
.
解法二:過A引BE的平行線,交CB的延長線于F.
∠DAF是異面直線BE與AD所成的角.
∴∠DAF=![]() .
.
∵E是AC的中點,∴B是CF的中點.
AF=2BE=![]() .
.
又BF、BA分別是DF、DA的射影,且BF=BC=BA,
∴DF=DA.
三角形ADF是等腰三角形,
AD=![]() ,
,
故BD=![]() .
.
又VABCD=![]() ,
,
因此四面體ABCD的體積是![]() .
.


科目:高中數學 來源: 題型:
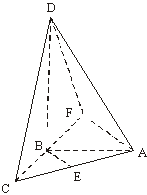
 在如圖所示的四面體ABCD中,AB、BC、CD兩兩互相垂直,且BC=CD=1.
在如圖所示的四面體ABCD中,AB、BC、CD兩兩互相垂直,且BC=CD=1.查看答案和解析>>
科目:高中數學 來源: 題型:
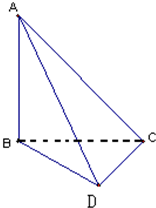
 (2009•襄陽模擬)在如圖所示的四面體ABCD中,AB、BC、CD兩兩互相垂直,且BC=CD=1.
(2009•襄陽模擬)在如圖所示的四面體ABCD中,AB、BC、CD兩兩互相垂直,且BC=CD=1.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,直角梯形ACDE與等腰直角△ABC所在平面互相垂直,F(xiàn)為BC的中點,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如圖所示,直角梯形ACDE與等腰直角△ABC所在平面互相垂直,F(xiàn)為BC的中點,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′兩兩垂直,E,F(xiàn),H分別是AC,AB,BC的中點,
如圖所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′兩兩垂直,E,F(xiàn),H分別是AC,AB,BC的中點,查看答案和解析>>
科目:高中數學 來源: 題型:
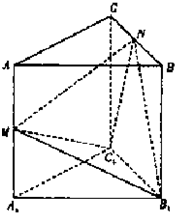 (2010•武漢模擬)如圖所示,在正三棱柱ABC-A1B1C1中,底面ABC的邊長為2a,側棱AA1=2a,M、N分別為AA1、BC中點
(2010•武漢模擬)如圖所示,在正三棱柱ABC-A1B1C1中,底面ABC的邊長為2a,側棱AA1=2a,M、N分別為AA1、BC中點查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com