
設曲線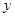 在點
在點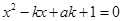 處的切線為
處的切線為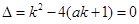 ,曲線
,曲線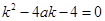 在點
在點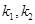 處的切線為
處的切線為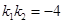 .若存在
.若存在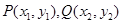 ,使得
,使得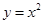 ,則實數
,則實數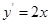 的取值范圍是 .
的取值范圍是 .
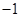
【解析】
試題分析:∴l1的斜率為k1=(ax0+a-1)ex0,函數y=(1-x)e-x的導數為y′=(x-2)e-x∴l2的斜率為k2=(x0-2)e-x0,由題設有k1?k2=-1從而有(ax0+a-1)ex0?(x0-2)e-x0=-1∴a(x02-x0-2)=x0-3∵x0∈[0,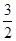 ]得到x02-x0-2≠0,所以a=
]得到x02-x0-2≠0,所以a=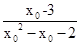 ,又a′=
,又a′=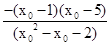 ,另導數大于0得1<x0<5,故
,另導數大于0得1<x0<5,故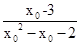 在(0,1)是減函數,在(1,
在(0,1)是減函數,在(1,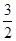 )上是增函數, x0=0時取得最大值為
)上是增函數, x0=0時取得最大值為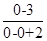 =
=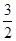 x0=1時取得最小值為1.∴1≤a≤
x0=1時取得最小值為1.∴1≤a≤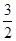 ,故答案為:
,故答案為: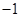
考點:用導數求切線的斜率
點評:此題是一道綜合題,考查學生會利用導數求切線的斜率,會求函數的值域,掌握兩直線垂直時斜率的關系.


科目:高中數學 來源: 題型:
(08年黃岡中學二模)函數![]() 關于直線
關于直線![]() 對稱的函數為
對稱的函數為![]() ,又函數
,又函數![]() 的導函數為
的導函數為![]() ,記
,記![]()
(1)設曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,若
,若![]() 與圓
與圓![]() 相切,求
相切,求![]() 的值;
的值;
(2)求函數![]() 的單調區間;
的單調區間;
(3)求函數![]() 在[0,1]上的最大值;
在[0,1]上的最大值;
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年黃岡中學二模)函數![]() 關于直線
關于直線![]() 對稱的函數為
對稱的函數為![]() ,又函數
,又函數![]() 的導函數為
的導函數為![]() ,記
,記![]()
(1)設曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,若
,若![]() 與圓
與圓![]() 相切,求
相切,求![]() 的值;
的值;
(2)求函數![]() 的單調區間;
的單調區間;
(3)求函數![]() 在[0,1]上的最大值;
在[0,1]上的最大值;
查看答案和解析>>
科目:高中數學 來源:2010年普通高等學校招生全國統一考試(重慶卷)數學理工類模擬試卷(三) 題型:解答題
函數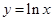 關于直線
關于直線 對稱的函數為
對稱的函數為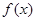 ,又函數
,又函數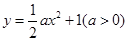 的導函數為
的導函數為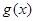 ,記
,記 .
.
(Ⅰ)設曲線 在點
在點 處的切線為
處的切線為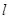 ,
,
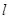 與圓
與圓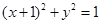 相切,求
相切,求 的值;
的值;
(Ⅱ)求函數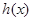 的單調區間;
的單調區間;
(Ⅲ)求函數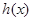 在[0,1]上的最大值.
在[0,1]上的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com