
已知二次函數f(x)=ax2+bx+c和一次函數g(x)=-bx,其中a、b、c滿足a>b>c,a+b+c=0,(a,b,c∈R).
(1)求證:兩函數的圖象交于不同的兩點A、B;
(2)求線段AB在x軸上的射影A1B1的長的取值范圍.
答案見解析
(1)證明:由![]() 消去y得ax2+2bx+c=0
消去y得ax2+2bx+c=0
Δ=4b2-4ac=4(-a-c)2-4ac=4(a2+ac+c2)=4[(a+![]() c2]
c2]
∵a+b+c=0,a>b>c,∴a>0,c<0
∴![]() c2>0,∴Δ>0,即兩函數的圖象交于不同的兩點.
c2>0,∴Δ>0,即兩函數的圖象交于不同的兩點.
(2)解:設方程ax2+bx+c=0的兩根為x1和x2,則x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
|A1B1|2=(x1-x2)2=(x1+x2)2-4x1x2
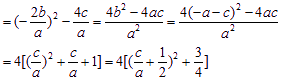
∵a>b>c,a+b+c=0,a>0,c<0
∴a>-a-c>c,解得![]() ∈(-2,-
∈(-2,-![]() )
)
∵![]() 的對稱軸方程是
的對稱軸方程是![]() .
.
![]() ∈(-2,-
∈(-2,-![]() )時,為減函數
)時,為減函數
∴|A1B1|2∈(3,12),故|A1B1|∈(![]() ).
).


科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| x |
| 1 |
| 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| bx-1 | a2x+2b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| bx-1 | a2x+2b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com