
已知函數 (b為常數).
(b為常數).
(1)函數f(x)的圖像在點(1,f(1))處的切線與g(x)的圖像相切,求實數b的值;
(2)設h(x)=f(x)+g(x),若函數h(x)在定義域上存在單調減區間,求實數b 的取值范圍;
(3)若b>1,對于區間[1,2]上的任意兩個不相等的實數x1,x2,都有|f(x1)-f(x2)|> |g(x1)-g(x2)|成立,求b的取值范圍.
(1)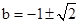 (2)
(2)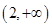 (3)
(3)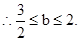
【解析】
試題分析:1)由f(x)求出其導函數,把切點的橫坐標代入導函數中即可表示出切線的斜率,根據切點坐標和切線過原點寫出切線方程,再和g(x)聯立,利用根的判別求解即可.(2)通過求h′(x),結合函數h(x)在定義域上存在單調減區間,轉化為存在性問題求b的取值范圍.(3)要使得對于區間[1,2]上的任意兩個不相等的實數x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,利用導數的幾何是切線的斜率,得到對于區間[1,2]上的任意實數x,|f′(x)|>|g′(x)|,列出b的不等關系,從而得出b的取值范圍.解:(1)f(x)=lnx得f′(x)=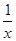 ,函數f(x)的圖象在點(1,f(1))處的切線的斜率為f′(1)=1,切線方程為:y-0=x-1即y=x-1.
,函數f(x)的圖象在點(1,f(1))處的切線的斜率為f′(1)=1,切線方程為:y-0=x-1即y=x-1.
由已知得它與g(x)的圖象相切,將y=x-1代入得x-1=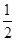 x2-bx,即
x2-bx,即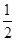 x2-(b+1)x+1=0,∴△=(b+1)2-2=0,解得b=±
x2-(b+1)x+1=0,∴△=(b+1)2-2=0,解得b=±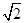 -1,即實數b的值為±
-1,即實數b的值為±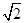 -1.(2)h(x)=f(x)+g(x)=lnx+
-1.(2)h(x)=f(x)+g(x)=lnx+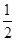 x2-bx,∴h′(x)=
x2-bx,∴h′(x)=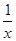 +x-b,根據函數h(x)在定義域(0,+∞)上存在單調減區間,∴存在x>0,使得
+x-b,根據函數h(x)在定義域(0,+∞)上存在單調減區間,∴存在x>0,使得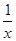 +x-b<0,即b>
+x-b<0,即b>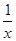 +x,由于當x>0時,
+x,由于當x>0時,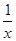 +x≥2,∴b>2.∴實數b 的取值范圍(2,+∞).
+x≥2,∴b>2.∴實數b 的取值范圍(2,+∞).
(3)對于區間[1,2]上的任意實數x,f′(x)=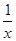 ∈[
∈[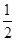 ,1]. g′(x)=x-b∈[1-b,2-b],要使得對于區間[1,2]上的任意兩個不相等的實數x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,若用注意到f(x)是增函數,不妨設x1>x2,則f(x1)>f(x2),問題轉化為|f(x1)-f(x2)|>|g(x1)-g(x2)|等價于-f(x1)+f(x2)<g(x1)-g(x2)<f(x1)-f(x2)從而f(x1)-g(x1)>f(x2)-g(x2)且f(x1)+g(x1)>f(x2)+g(x2),即f(x)-g(x)與f(x)+g(x)都是增函數,利用導數的幾何是切線的斜率,得到|f′(x)|>|g′(x)|,即
,1]. g′(x)=x-b∈[1-b,2-b],要使得對于區間[1,2]上的任意兩個不相等的實數x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,若用注意到f(x)是增函數,不妨設x1>x2,則f(x1)>f(x2),問題轉化為|f(x1)-f(x2)|>|g(x1)-g(x2)|等價于-f(x1)+f(x2)<g(x1)-g(x2)<f(x1)-f(x2)從而f(x1)-g(x1)>f(x2)-g(x2)且f(x1)+g(x1)>f(x2)+g(x2),即f(x)-g(x)與f(x)+g(x)都是增函數,利用導數的幾何是切線的斜率,得到|f′(x)|>|g′(x)|,即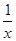 >|b-x|,于是x-
>|b-x|,于是x-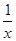 ≤b≤x+
≤b≤x+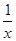 即(x-
即(x-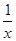 )max≤b≤(x+
)max≤b≤(x+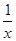 )min,∴
)min,∴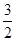 ≤b≤2.則b的取值范圍[
≤b≤2.則b的取值范圍[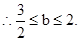 (1)
(1)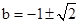 ;
;
(2)b的取值范圍為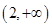
考點:函數單調性
點評:對于已知函數單調性,求參數范圍問題的常見解法;設函數f(x)在(a,b)上可導,若f(x)在(a,b)上是增函數,則可得f′(x)≥0,從而建立了關于待求參數的不等式,同理,若f(x)在(a,b)上是減函數,,則可得f′(x)≤0.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2011-2012學年四川省綿陽市高三第二次月考文科數學試卷 題型:解答題
已知函數 ,a,b為常數,
,a,b為常數,
(1) 若曲線 %
% 在點(2, 0)處有相同的切線,求a,b的值;
在點(2, 0)處有相同的切線,求a,b的值;
(2) 當 且
且 時,函數
時,函數 在
在 上有最小值,求實數a的取值范圍.
上有最小值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省深圳市南山區高三(上)期末數學試卷(理科)(解析版) 題型:解答題
 ,b為常數,b∈R,且
,b為常數,b∈R,且 是方程f(x)=0的解.
是方程f(x)=0的解.查看答案和解析>>
科目:高中數學 來源:2008年上海市奉賢區高考數學二模試卷(文科)(解析版) 題型:解答題
 ,b為常數,b∈R,且
,b為常數,b∈R,且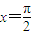 是方程f(x)=0的解.
是方程f(x)=0的解.查看答案和解析>>
科目:高中數學 來源:2008-2009學年廣東省深圳外國語學校高三第二次質量檢測數學試卷(理科)(解析版) 題型:解答題
 ,b為常數,b∈R,且
,b為常數,b∈R,且 是方程f(x)=0的解.
是方程f(x)=0的解.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com