


科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 3 |
| 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π | 2 |
查看答案和解析>>
科目:高中數學 來源:2007年普通高等學校招生全國統一考試理科數學卷(江西) 題型:解答題
(本小題滿分12分)
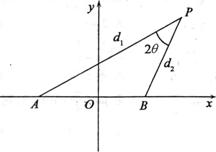
設動點P到點A(-l,0)和B(1,0)的距離分別為d1和d2,
∠APB=2θ,且存在常數λ(0<λ<1=,使得d1d2 sin2θ=λ.
(1)證明:動點P的軌跡C為雙曲線,并求出C的方程;
(2)過點B作直線交雙曲線C的右支于M、N兩
點,試確定λ的范圍,使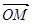 ·
·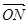 =0,其中點
=0,其中點
O為坐標原點.
查看答案和解析>>
科目:高中數學 來源:《第3章 不等式》2011年單元測試卷(蒼南中學)(解析版) 題型:解答題
 ;
; .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com