
 ,則( )
,則( ) 上單調遞增
上單調遞增 對稱
對稱 對稱
對稱 ,k∈Z,即可對于選項C作出判斷;由正弦函數的對稱中心為kπ,k∈Z,即可對于選項D作出判斷.
,k∈Z,即可對于選項C作出判斷;由正弦函數的對稱中心為kπ,k∈Z,即可對于選項D作出判斷.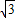 cos2x=
cos2x= sin2x-
sin2x-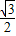 (cos2x+1)=sin(2x-
(cos2x+1)=sin(2x-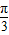 )-
)-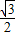 ,
,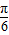 ,
,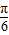 ],∴2x-
],∴2x-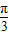 ∈[-
∈[- ,0],
,0],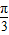 ∈[-
∈[-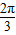 ,-
,-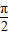 ]時,f(x)單調遞減;當2x+
]時,f(x)單調遞減;當2x+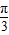 ∈[-
∈[-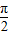 ,0]時,f(x)單調遞增,
,0]時,f(x)單調遞增,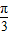 =kπ+
=kπ+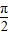 ,k∈Z,解得:x=
,k∈Z,解得:x= kπ+
kπ+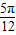 ,k∈Z,
,k∈Z,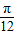 ,即函數f(x)的圖象關于直線x=-
,即函數f(x)的圖象關于直線x=-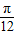 對稱,故選項C正確;
對稱,故選項C正確;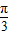 =kπ,k∈Z,解得:x=
=kπ,k∈Z,解得:x= kπ+
kπ+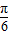 ,k∈Z,
,k∈Z,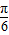 ,可得函數圖象關于(
,可得函數圖象關于(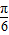 ,-
,-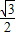 )對稱,故選項D錯誤,
)對稱,故選項D錯誤,

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com