Question

已知定義在R上的偶函數y=f（x）滿足：f（x+4）=f（x）+f（2），且當x∈[0，2]時，y=f（x）單調遞減，給出以下四個命題：
①f（2）=0；             
②x=-4為函數y=f（x）圖象的一條對稱軸；
③函數y=f（x）在[8，10]單調遞增；
④若關于x的方程f（x）=m在[一6，一2]上的兩根為x₁，x₂，則x₁+x₂=-8．
以上命題中所有正確的命題為（ ）
A．①②④
B．①③④
C．②④
D．③④

Answer 1

【答案】分析：根據f（x）是定義在R上的偶函數，及在f（x+4）=f（x）+f（2），中令x=-2可得f（-2）=f（2）=0，從而有f（x+4）=f（x），故得函數f（x）是周期為4的周期函數，再結合y=f（x）單調遞減、奇偶性畫出函數f（x）的簡圖，最后利用從圖中可以得出正確的結論．
解答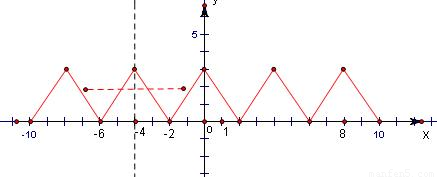：解：∵f（x）是定義在R上的偶函數，
∴f（-x）=f（x），
可得f（-2）=f（2），
在f（x+4）=f（x）+f（2），中令x=-2得
f（2）=f（-2）+f（2），
∴f（-2）=f（2）=0，
∴f（x+4）=f（x），
∴函數f（x）是周期為4的周期函數，
又當x∈[0，2]時，y=f（x）單調遞減，結合函數的奇偶性畫出函數f（x）的簡圖，如圖所示．
從圖中可以得出：
②x=-4為函數y=f（x）圖象的一條對稱軸；
③函數y=f（x）在[8，10]單調遞減；
④若方程f（x）=m在[-6，-2]上的兩根為x₁，x₂，則x₁+x₂=-8．
故①②④正確；
故選A；
點評：本題考查函數奇偶性的性質，函數奇偶性的判斷，考查學生的綜合分析與轉化能力，屬于難題．