Question

【題目】某園林基地培育了一種新觀賞植物，經(jīng)過一年的生長發(fā)育，技術(shù)人員從中抽取了部分植株的高度（單位：厘米）作為樣本（樣本容量為）進(jìn)行統(tǒng)計，按照 的分組作出頻率分布直方圖，并作出樣本高度的莖葉圖（圖中僅列出了高度在的數(shù)據(jù)）.

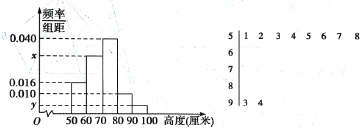
（1）求樣本容量和頻率分布直方圖中的的值；

（2）在選取的樣本中，從高度在厘米以上（含厘米）的植株中隨機(jī)抽取株，求所取的株中至少有一株高度在內(nèi)的概率.

Answer 1

【答案】（1）；（2）；

【解析】試題分析：（1）由莖葉圖可知中的樣本有個，其頻率為，由此可求出，因為有個，其頻率為，則，根據(jù)頻率之和為，可求出；（2）根據(jù)（1）可知高度在內(nèi)株數(shù)為，高度在內(nèi)的株數(shù)為，列出所有情況共種，符合的有種，即可求出．理解題意后列舉出所有情況即可．

試題解析：（1）由題意可知, 樣本容量,.

（2）由題意可知, 高度在內(nèi)株數(shù)為,記這株分別為,高度在內(nèi)的株數(shù)為,記株分別為.抽取株的所有情況有種, 分別為,,,,其中株的高度都不在內(nèi)的情況有種分別為 ,所抽取的株中至少有一株高度在內(nèi)的概率.