
(12分)已知函數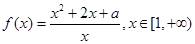
(Ⅰ)當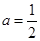 時,求函數
時,求函數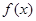 的最小值;
的最小值;
(Ⅱ)若對任意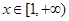 ,
,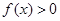 恒成立,試求實數
恒成立,試求實數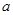 的取值范圍.
的取值范圍.
(Ⅰ) 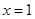 時,
時,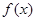 取得最小值
取得最小值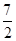 .(Ⅱ)
.(Ⅱ) 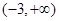 .
.
【解析】
試題分析:(1)先將原式化成求解導數f‘(x),再利用導數的正負與函數單調性的關系,即可求得函數f(x)的最小值;
(2)原題等價于x2+2x+a>0對x∈[1,+∞)恒成立,再結合二次函數的單調性只須g(1)>0,從而求得實數a的取值范圍;
解(Ⅰ) 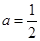 時,
時,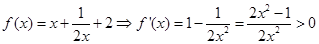 (因為
(因為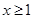 )
)
所以,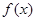 在
在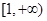 上單調遞增,故
上單調遞增,故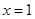 時,
時,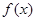 取得最小值
取得最小值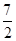 .
.
(Ⅱ) 因為對任意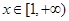 ,
,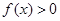 恒成立,即
恒成立,即 恒成立,只需
恒成立,只需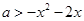 恒成立,只需
恒成立,只需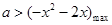 ,因為
,因為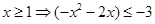 ,
,
所以,實數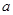 的取值范圍是
的取值范圍是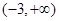 .
.
考點:本題主要考查了函數單調性的應用、函數奇偶性的應用、不等式的解法等基礎知識,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于基礎題.
點評:解決該試題的關鍵是是對于同一個問題的不同的處理角度,可以運用均值不等式得到最值,也可以結合導數的工具得到最值,對于恒成立問題一般都是轉換為求解函數的 最值即可得到。


科目:高中數學 來源:2011屆廣東省深圳高級中學高三高考最后模擬考試文數 題型:解答題
(本小題滿分14分)已知函數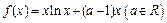 .
.
(Ⅰ)當 時,求曲線
時,求曲線 在
在 處的切線方程;
處的切線方程;
(Ⅱ)求函數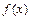 在區間
在區間 上的最小值;
上的最小值;
(Ⅲ)若關于的方程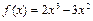 在區間
在區間 內有兩個不相等的實數根,求實數a的取值范圍.
內有兩個不相等的實數根,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省天水市高三第三次考試文科數學試卷(解析版) 題型:解答題
(本小題10分)已知函數 當
當 時,求不等式
時,求不等式 的解集;若
的解集;若 的解集包含
的解集包含 ,求a的取值范圍。
,求a的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com