分析:(1)法一:由于λ不確定,從而E點是個動點,而要A
1C⊥平面BED,所以不妨考慮A
1C⊥平面BED滿足的條件,從而發現必須有A
1C⊥BE,由三垂線定理,得到B
1C⊥BE,由三角形相似容易得到λ的值,
法二:用向量法,以D為坐標原點,射線DA為x軸的正半軸,射線DC為y軸的正半軸,射線DD
1為z軸的正半軸,建立如圖所示直角坐標系D-xyz.則:D(0,0,0),B(2,2,0),C(0,2,0),A
1(2,0,4),由于CE=λCC
1,而CC
1的坐標可求,A
1C坐標可求,若A
1C⊥平面BED,則A
1C⊥DE,由向量內積定義可求λ的值;
(2)法一:在解決問題(1)的基礎上,可以作出二面角的平面角,通過解三角形解決.
法二:用向量法,由(1)知平面BDE的一個法向量為
=(-2,2,-4),故只需求平面DA
1B的一個法向量,設為n=(x,y,z),則n⊥
,n⊥
,通過內積為0求之,再計算向量n與向量A
1C的夾角即可.
解答:解:法一:(1)連接B
1C交BE于點F,連接AC交BD于點G,
∴AC⊥BD,由垂直關系得,A
1C⊥BD,
若A
1C⊥平面BED,則A
1C⊥BE,
由垂直關系可得B
1C⊥BE,
∴△BCE∽△B
1BC,∴
=
=
,
∴CE=1,∴λ=
=
.
(2)連接A
1G,連接EG交A
1C于H,則A
1G⊥BD.
∵A
1C⊥平面BED,
∴∠A
1GE是二面角A
1-BD-E的平面角.
∵A
1G=3
,EG=
,A
1E=
,
∴cos∠A
1GE=
=
,
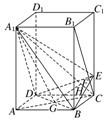
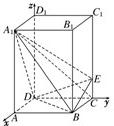
法二:(1)以D為坐標原點,射線DA為x軸的正半軸,射線DC為y軸的正半軸,射線DD
1為z軸的正半軸,建立如圖所示直角坐標系D-xyz.
依題設,D(0,0,0),B(2,2,0),C(0,2,0),A
1(2,0,4),
∵CE=λCC
1=4λ,∴E(0,2,4λ),
∴
=(2,2,0),
=(2,0,4),
=(-2,2,-4),
=(0,2,4λ),
∵
•
=2×(-2)+2×2+0×(-4)=0,
∴
⊥
,∴DB⊥A
1C.
若A
1C⊥平面BED,則A
1C⊥DE,∴
⊥
,
∴
•
=(-2)×0+2×2+(-4)×4λ=4-16λ=0,
∴λ=
.
(2)設向量n=(x,y,z)是平面DA
1B的一個法向量,
則n⊥
,n⊥
,∴2x+2y=0,2x+4z=0,
令z=1,則x=-2,y=2,∴n=(-2,2,1)
由(1)知平面BDE的一個法向量為
=(-2,2,-4)
∴cos<n,
>=
=
.
即二面角A
1-BD-E的余弦值為
.
點評:本題考查直線垂直于平面、二面角的求法,在長方體、正方體等較為規則的幾何體中,因為容易建立空間坐標系,可以考慮向量法解決,也可以用幾何法推導,但是一定要注意問題中有連續的幾問時,前一問對后面問題的影響,從而使后面的問題的解決變得簡捷.

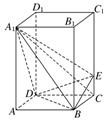 如圖,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,點E在CC1上,且CE=λCC1.
如圖,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,點E在CC1上,且CE=λCC1.



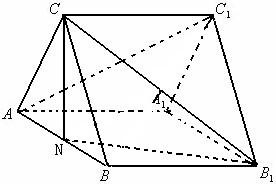 如圖是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N為棱AB中點.
如圖是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N為棱AB中點.
 如圖是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N為棱AB中點.
如圖是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N為棱AB中點.
