
設集合Sn={1,2,3,,n),若X是Sn的子集,把X中所有元素的和稱為X的“容量”(規定空集的容量為0),若X的容量為奇(偶)數,則稱X為Sn的奇(偶)子集.
(I)寫出S4的所有奇子集;
(Ⅱ)求證:Sn的奇子集與偶子集個數相等;
(Ⅲ)求證:當n≥3時,Sn的所有奇子集的容量之和等于所有偶子集的容量之和.
(I)詳見解析;(Ⅱ)詳見解析;(Ⅲ)詳見解析
解析試題分析:(I)根據奇子集的定義可直接得出,注意應按規律一一列出以防重寫或漏寫。(Ⅱ)取Sn的任意一個奇子集 可能含有1也可能不含1,當奇子集
可能含有1也可能不含1,當奇子集 含有1時,令
含有1時,令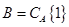 ,當奇子集
,當奇子集 不含1時,令
不含1時,令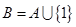 ,則
,則 為
為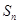 的偶子集,且
的偶子集,且 與
與 相對應,反之也成立。因為
相對應,反之也成立。因為 與
與 相對應即Sn的奇子集與偶子集個數相等。(Ⅲ)由(Ⅱ)知Sn的奇子集與偶子集個數相等,且Sn中每一個元素在奇子集與偶子集中出現的次數是相同的,所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
相對應即Sn的奇子集與偶子集個數相等。(Ⅲ)由(Ⅱ)知Sn的奇子集與偶子集個數相等,且Sn中每一個元素在奇子集與偶子集中出現的次數是相同的,所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
試題解析:(I)
(Ⅱ)對于Sn的每個奇子集 ,
,
當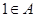 時,取
時,取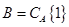 ;當
;當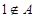 時,取
時,取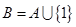 。
。
則 為
為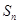 的偶子集。
的偶子集。
反之,若 為
為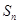 的偶子集,
的偶子集,
當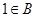 時,取
時,取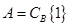 ;當
;當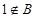 時,取
時,取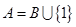 。
。
則 為
為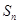 的奇子集。
的奇子集。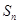 的奇子集與偶子集之間建立了一一對應的關系,所以
的奇子集與偶子集之間建立了一一對應的關系,所以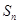 的奇子集和偶子集的個數相等。
的奇子集和偶子集的個數相等。
(Ⅲ)對于任意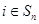 ,
,
當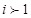 時,含
時,含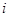 的
的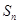 的子集共有
的子集共有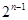 個。由(Ⅱ)可知,對每個數
個。由(Ⅱ)可知,對每個數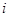
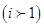 ,在奇子集與偶子集中,
,在奇子集與偶子集中,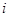 所占的個數是相等的;
所占的個數是相等的;
當 時,將(Ⅱ)中的1換成3即可。
時,將(Ⅱ)中的1換成3即可。
可知 在奇子集與偶子集中占的個數是相等。
在奇子集與偶子集中占的個數是相等。
綜合(1)(2),每個元素都是在奇子集與偶子集中占的個數相等。
所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
考點:新概念問題。


科目:高中數學 來源: 題型:填空題
已知集合A、B,定義集合A與B的一種運算A⊕B,其結果如下表所示:
| A | {1,2,3,4} | {-1,1} | {-4,8} | {-1,0,1} |
| B | {2,3,6} | {-1,1} | {-4,-2,0,2} | {-2,-1,0,1} |
| A⊕B | {1,4,6} | ∅ | {-2,0,2,8} | {-2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m-1}.
(1) 若B A,求實數m的取值范圍;
A,求實數m的取值范圍;
(2) 當x∈R時,沒有元素x使x∈A與x∈B同時成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知集合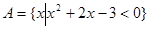 ,
,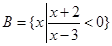 .
.
(1)在區間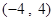 上任取一個實數
上任取一個實數 ,求“
,求“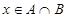 ”的概率;
”的概率;
(2)設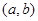 為有序實數對(如有序實數對(2,3)與(3,2)不一樣),其中
為有序實數對(如有序實數對(2,3)與(3,2)不一樣),其中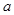 是從集合
是從集合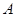 中任取的一個整數,
中任取的一個整數,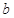 是從集合
是從集合 中任取的一個整數,求“
中任取的一個整數,求“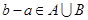 ”的概率
”的概率
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
設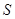 為復數集
為復數集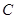 的非空子集.若對任意
的非空子集.若對任意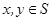 ,都有
,都有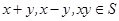 ,則稱S為封閉集.下列命題:①集合S={a+bi|(
,則稱S為封閉集.下列命題:①集合S={a+bi|(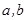 為整數,
為整數,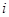 為虛數單位)}為封閉集;②若S為封閉集,則一定有
為虛數單位)}為封閉集;②若S為封閉集,則一定有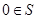 ;③封閉集一定是無限集;④若
;③封閉集一定是無限集;④若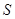 為封閉集,則滿足
為封閉集,則滿足 的任意集合
的任意集合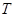 也是封閉集.其中真命題是 (寫出所有真命題的序號).
也是封閉集.其中真命題是 (寫出所有真命題的序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com