Question

已知函數f(x)=log_ax和g(x)=2log_a(2x+t-2)，(a＞0，a≠1，t∈R)的圖像在x=2處的切線互相平行.

(Ⅰ)求t的值；

(Ⅱ)設F(x)=g(x)-f(x)，當x∈[1，4]時，F(x)≥2恒成立，求a的取值范圍.

Answer 1

解：(Ⅰ)∵f′(x)=log_ae,g′(x)=log_ae 

∵函數f(x)和g(x)的圖像在x=2處的切線互相平行∴f′(2)=g′(2) 

∴log_ae=log_ae  ∴t=6

(Ⅱ)∵t=6∴F(x)=g(x)-f(x)=2log_a(2x+4)-log_ax=log_a,x∈[1,4]

令h(x)=4-=4x++16,x∈[1,4]

∵h′(x)=4-=,x∈[1,4]

∴當1≤x＜2時,h′(x)＜0,當2＜x≤4時,h′(x)＞0.

∴h(x)在[1,2)是單調減函數,在(2,4]是單調增函數.

∴h(x)_min=h(2)=32,∴h(x)_max=h(1)=h(4)=36

∴當0＜a＜1時,有F(x)_min=log_a36,當a＞1時,有F(x)_min=log_a32.

∵當x∈[1,4]時,F(x)≥2恒成立,∴F(x)_min≥2 

∴滿足條件的a的值滿足下列不等式組

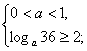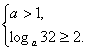  ①,或   ②

不等式組①的解集為空集,解不等式組②得1＜a≤

綜上所述,滿足條件的a的取值范圍是：1＜a≤.