
已知圓M:(![]() +
+![]() )2+y2=36,定點N(
)2+y2=36,定點N(![]() ,0),點P為圓M上的動點,點Q在NP上,點G在MP上,且滿足
,0),點P為圓M上的動點,點Q在NP上,點G在MP上,且滿足![]() ,
,![]() .
.
(1)求點G的軌跡C的方程;
(2)過點(2,0)作直線![]() ,與曲線C交于A、B兩點,O是坐標原點,設
,與曲線C交于A、B兩點,O是坐標原點,設![]() ,是否存在這樣的直線
,是否存在這樣的直線![]() ,使四邊形OASB的對角線相等(即
,使四邊形OASB的對角線相等(即![]() )?若存在,求出直線
)?若存在,求出直線![]() 的方程;若不存在。說明理由。
的方程;若不存在。說明理由。
解:(1)由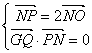
得Q為PN的中點且GQ⊥PN,所以GQ為PN的中垂線.
因此|PG|=|GN|,從而|GN| + |GM|=|MP|=6,
故G點的軌跡是以M、N為焦點的橢圓,其長半軸長![]() =3,半焦距
=3,半焦距![]() ,
,
所以短半軸長b=2,所以點G的軌跡方程是![]() .
.
(2)因為![]() ,所以四邊形OASB為平行四邊形.
,所以四邊形OASB為平行四邊形.
若存在直線![]() 使得
使得![]() ,則四邊形OASB為矩形,所以
,則四邊形OASB為矩形,所以![]() .
.
若直線![]() 的斜率不存在,直線
的斜率不存在,直線![]() 的方程為
的方程為![]() =2,
=2,
由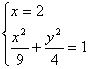 ,得
,得
所以![]() ,這與
,這與![]() 矛盾,
矛盾,
故直線![]() 的斜率存在.
的斜率存在.
設直線![]() 的方程為y=k(
的方程為y=k(![]() -2),A(
-2),A(![]() 1,yl)、B(
1,yl)、B(![]() 2,y2),
2,y2),
由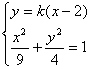 得
得
(9k2+4) ![]() 2-36k2
2-36k2![]() +36(k2―1)=0.
+36(k2―1)=0.
所以![]() ,
,![]() ①
①
故![]() ②
②
把式①、②代入![]() ,解得
,解得![]() .
.
∴存在直線![]() :3
:3![]() -2y-6=0或3
-2y-6=0或3![]() +2y-6=0
+2y-6=0
使得四邊形OASB的對角線相等.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
已知圓M:(x-![]() )2+y2=
)2+y2=![]() ,若橢圓C:
,若橢圓C:![]() +
+![]() =1(a>b>0)的右頂點為圓M的圓心,離心率為
=1(a>b>0)的右頂點為圓M的圓心,離心率為![]() .
.
(1)求橢圓C的方程.
(2)已知直線l:y=kx,若直線l與橢圓C分別交于A,B兩點,與圓M分別交于G,H兩點(其中點G在線段AB上),且|AG|=|BH|,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知圓M:(x-![]() )2+y2=
)2+y2=![]() ,若橢圓C:
,若橢圓C:![]() +
+![]() =1(a>b>0)的右頂點為圓M的圓心,離心率為
=1(a>b>0)的右頂點為圓M的圓心,離心率為![]() .
.
(1)求橢圓C的方程.
(2)已知直線l:y=kx,若直線l與橢圓C分別交于A,B兩點,與圓M分別交于G,H兩點(其中點G在線段AB上),且|AG|=|BH|,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知圓M:(![]() +
+![]() )2+y2=36,定點N(
)2+y2=36,定點N(![]() ,0),點P為圓M上的動點,點Q在NP上,點G在MP上,且滿足
,0),點P為圓M上的動點,點Q在NP上,點G在MP上,且滿足![]() ,
,![]() =0.
=0.
(1)求點G的軌跡C的方程;
(2)過點(2,0)作直線![]() ,與曲線C交于A、B兩點,O是坐標原點,
,與曲線C交于A、B兩點,O是坐標原點,![]() ,是否存在這樣的直線
,是否存在這樣的直線![]() ,使四邊形OASB的對角線相等(即
,使四邊形OASB的對角線相等(即![]() )?若存在,求出直線
)?若存在,求出直線![]() 的方程;若不存在.說明理由.
的方程;若不存在.說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com