【題目】已知函數
.
（1）討論
的單調性；
（2）若有兩個零點，求
的取值范圍.
【答案】（1）詳見解析；（2）
.
【解析】
（1）由題意知：取得函數的導數，分類討論，即可求解函數的單調區間；
（2）由（1）知當
和
時，不合題意； 當
時，要使得要使
有兩個零點，必有
，構造新函數
，利用導數求得函數函數的單調性和最值，即可得到結論.
解：（1）由題意知：
若
，即
時，在
上單減，在
單增
若
，即
時，
當
時，在
單增；
當
時，在
上單增，在
單減，在上單增；
當
時，在上單增，在
單減，在
上單增.
（2）由（1）知當時，在單增，故不可能有兩個零點.
當
時，
只有一個零點，不合題意.
當
時，在上單減，在單增，且
時，
；
時，.
故只要
，解得：
.
當時，在上單增，在單減，在上單增.
因為
故也不可能有兩個零點.
當時，在上單增，在單減，在上單增
且，故要使有兩個零點，必有
由
即當時，有
因為
即
在
上單增，且時，
.
故當時，不可能有兩個零點.
綜上所述：當時，有兩個零點.
科目：高中數學 來源： 題型：
【題目】為更好地落實農民工工資保證金制度，南方某市勞動保障部門調查了
年下半年該市
名農民工（其中技術工、非技術工各
名）的月工資，得到這名農民工月工資的中位數為
百元（假設這名農民工的月工資均在
（百元）內）且月工資收入在
（百元）內的人數為
，并根據調查結果畫出如圖所示的頻率分布直方圖：
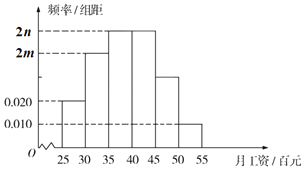
（Ⅰ）求
，
的值；
（Ⅱ）已知這名農民工中月工資高于平均數的技術工有
名，非技術工有
名，則能否在犯錯誤的概率不超過
的前提下認為是不是技術工與月工資是否高于平均數有關系？
參考公式及數據：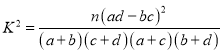
，其中
．
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
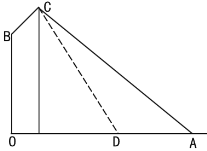
【題目】如圖，在路邊安裝路燈：路寬
米，燈桿長
米，且與燈柱
成120°角，路燈采用錐形燈罩，燈罩軸線
與燈桿垂直且正好通過道路路面的中線.
（1）求燈柱高的長度（精確到0.01米）；
（2）若該路燈投射出的光成一個圓錐體，該圓錐體母線與軸線的夾角是30°，寫出路燈在路面上投射出的截面圖形的邊界是什么曲線？寫出其相應的幾何量（精確到0.01米）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是( )
A.在線性回歸分析中，相關系數r的值越大，變量間的相關性越強
B.自變量取值一定時，因變量的取值帶有一定隨機性的兩個變量之間的關系叫做相關關系
C.在殘差圖中，殘差點分布的帶狀區域的寬度越狹窄，其模型擬合的精度越高
D.在問歸分析中，
為0.98的模型比為0.80的模型擬合的效果好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
過點
(
為非零常數)與
軸不垂直的直線
與C交于
兩點.
(1)求證:
(
是坐標原點)；
(2)AB的垂直平分線與軸交于
，求實數
的取值范圍；
(3)設A關于軸的對稱點為D,求證:直線BD過定點,并求出定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某中學甲、乙兩班各隨機抽取
名同學，測量他們的身高（單位：
），所得數據用莖葉圖表示如下，由此可估計甲、乙兩班同學的身高情況，則下列結論正確的是（ ）
A. 甲班同學身高的方差較大 B. 甲班同學身高的平均值較大
C. 甲班同學身高的中位數較大 D. 甲班同學身高在
以上的人數較多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
（
）的焦距為4，其短軸的兩個端點與長軸的一個端點構成正三角形.
（1）求橢圓
的標準方程；
（2）設
為橢圓的左焦點，直線
，
為橢圓上任意一點，證明：點到的距離是點到
距離的
倍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
