
求半徑為4,與圓x2+y2―4x―2y―4=0相切,且和直線y=0相切的圓的方程.
解:由題意,所求圓與直線y=0相切,且半徑為4,
則圓心坐標為O1(a,4),O1(a,-4).
又已知圓x2+y2―4x―2y―4=0的圓心為O2(2,1),半徑為3,
①若兩圓內切,則|O1O2|=4-3=1.
即(a-2)2+(4-1)2=12,或(a-2)2+(-4-1)2=12.
顯然兩方程都無解.
②若兩圓外切,則|O1O2|=4+3=7.
即(a-2)2+(4-1)2=72,或(a-2)2+(-4-1)2=72.
解得a=2±2![]() ,或a=2±2
,或a=2±2![]() .
.
∴所求![]() 圓的方程為
圓的方程為
(x―2―2![]() )2+(y-4)2=16或(x-2+2
)2+(y-4)2=16或(x-2+2![]() )2+(y-4)2=16;
)2+(y-4)2=16;
或(x―2―2![]() )2+(y+4)2=16或(x―2+2
)2+(y+4)2=16或(x―2+2![]() )2+(y+4)2=16.
)2+(y+4)2=16.


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 6 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省荊州中學高二(上)期中數學試卷(理科)(解析版) 題型:解答題
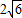 ,求圓C的方程.
,求圓C的方程.查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省荊州中學高二(上)期中數學試卷(理科)(解析版) 題型:解答題
 ,求圓C的方程.
,求圓C的方程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com