
【題目】已知數列![]() 滿足:對任意
滿足:對任意![]() ,若
,若![]() ,則
,則![]() ,且
,且![]() ,設
,設![]() ,集合
,集合![]() 中元素的最小值記為
中元素的最小值記為![]() ;集合
;集合![]() ,集合
,集合![]() 中元素最小值記為
中元素最小值記為![]() .
.
(1)對于數列:![]() ,求
,求![]() ,
,![]() ;
;
(2)求證:![]() ;
;
(3)求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)證明見解析;(3)416
(2)證明見解析;(3)416
【解析】
(1)根據題目,直接代入求解即可.
(2)利用反正法進行證明即可.
(3)欲使![]() 盡可能大,則任意連續三項和要盡量整體控制大,然后,分類討論即可進行求解
盡可能大,則任意連續三項和要盡量整體控制大,然后,分類討論即可進行求解
(1)![]()
(2)若![]() ,記
,記![]()
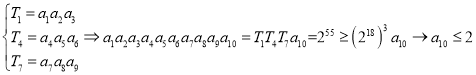
則![]() ,同樣操作
,同樣操作![]() 這三組數據得到
這三組數據得到![]() ,這與
,這與![]() ,
,![]() 矛盾,則
矛盾,則
![]() ,構造數列:
,構造數列:![]()
(3)欲使![]() 盡可能大,則任意連續三項和要盡量整體控制大,
盡可能大,則任意連續三項和要盡量整體控制大,![]() 如果放在數列中前
如果放在數列中前
后各有2個數,則![]() 這里對應含有
這里對應含有![]() 項的3個連續和,這3個和值顯然均大于
項的3個連續和,這3個和值顯然均大于![]() ,
,
同理也去控制![]() 項有
項有![]() ,這3個和值顯然均大于
,這3個和值顯然均大于![]() ,如果我們保證這6項不重疊,
,如果我們保證這6項不重疊,
則8個和,就先處理了6個,剩下2個要使得最小值最大,就有如圖排列這種排列:
![]() ,則
,則![]()
考慮![]() 其中
其中![]() ,這一組的和記
,這一組的和記
![]()
可以很快得到![]()
記![]() ,若
,若![]() ,則
,則![]() 這8個數字都要大于等于448,
這8個數字都要大于等于448,
![]() 至多各對應3個數字,
至多各對應3個數字,![]() 對應一個數字,那么這樣最多只有7個數字大于等于448,矛盾
對應一個數字,那么這樣最多只有7個數字大于等于448,矛盾
構造數列:![]() ,則
,則![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】武漢市掀起了轟轟烈烈的“十日大會戰”,要在10天之內,對武漢市民做一次全員檢測,徹底摸清武漢市的詳細情況.某醫院為篩查冠狀病毒,需要檢驗血液是否為陽性,現有![]() 份血液樣本,有以下兩種檢驗方式:
份血液樣本,有以下兩種檢驗方式:
方案①:將每個人的血分別化驗,這時需要驗1000次.
方案②:按![]() 個人一組進行隨機分組,把從每組
個人一組進行隨機分組,把從每組![]() 個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這
個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這![]() 個人的血就只需檢驗一次(這時認為每個人的血化驗
個人的血就只需檢驗一次(這時認為每個人的血化驗![]() 次);否則,若呈陽性,則需對這
次);否則,若呈陽性,則需對這![]() 個人的血樣再分別進行一次化驗這樣,該組
個人的血樣再分別進行一次化驗這樣,該組![]() 個人的血總共需要化驗
個人的血總共需要化驗![]() 次. 假設此次檢驗中每個人的血樣化驗呈陽性的概率為
次. 假設此次檢驗中每個人的血樣化驗呈陽性的概率為![]() ,且這些人之間的試驗反應相互獨立.
,且這些人之間的試驗反應相互獨立.
(1)設方案②中,某組![]() 個人中每個人的血化驗次數為
個人中每個人的血化驗次數為![]() ,求
,求![]() 的分布列;
的分布列;
(2)設![]() . 試比較方案②中,
. 試比較方案②中,![]() 分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案①,化驗次數最多可以減少多少次?(最后結果四舍五入保留整數)
分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案①,化驗次數最多可以減少多少次?(最后結果四舍五入保留整數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,過點
,過點![]() 作互相垂直的兩條直線分別交橢圓
作互相垂直的兩條直線分別交橢圓![]() 于點
于點![]() (
(![]() 與
與![]() 不重合).
不重合).
(1)證明:直線![]() 過定點
過定點![]() ;
;
(2)若以點![]() 為圓心的圓與直線
為圓心的圓與直線![]() 相切,且切點為線段
相切,且切點為線段![]() 的中點,求四邊形
的中點,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() (
(![]() 為坐標原點)的面積為
為坐標原點)的面積為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)如圖,點![]() 為橢圓上一動點(非長軸端點)
為橢圓上一動點(非長軸端點)![]() ,
,![]() 為左、右焦點,
為左、右焦點,![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,
點,![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,求
點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“扶貧幫困”是中華民族的傳統美德,某大型企業為幫扶貧困職工,設立“扶貧幫困基金”,采用如下方式進行一次募捐:在不透明的箱子中放入大小均相同的白球六個,紅球三個,每位獻愛心的參與者投幣100元有一次摸獎機會,一次性從箱中摸球三個(摸完球后將球放回),若有一個紅球,獎金20元,兩個紅球獎金40元,三個全為紅球獎金200元.
(1)求一位獻愛心參與者不能獲獎的概率;
(2)若該次募捐有300位獻愛心參與者,求此次募捐所得善款的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,
的左、右焦點,![]() 、
、![]() 兩點分別是橢圓
兩點分別是橢圓![]() 的上、下頂點,
的上、下頂點,![]() 是等腰直角三角形,延長
是等腰直角三角形,延長![]() 交橢圓
交橢圓![]() 于
于![]() 點,且
點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的動點,直線
的動點,直線![]() 、
、![]() 與直線
與直線![]() 分別相交于
分別相交于![]() 、
、![]() 兩點,點
兩點,點![]() ,試問:
,試問:![]() 外接圓是否恒過
外接圓是否恒過![]() 軸上的定點(異于點
軸上的定點(異于點![]() )?若是,求該定點坐標;若否,說明理由.
)?若是,求該定點坐標;若否,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com