
【題目】已知拋物線![]() 過點(diǎn)
過點(diǎn)![]() ,且焦點(diǎn)為
,且焦點(diǎn)為![]() ,直線
,直線![]() 與拋物線相交于
與拋物線相交于![]() 兩點(diǎn).
兩點(diǎn).
(1)求拋物線![]() 的方程,并求其準(zhǔn)線方程;
的方程,并求其準(zhǔn)線方程;
(2)若直線![]() 經(jīng)過拋物線
經(jīng)過拋物線![]() 的焦點(diǎn)
的焦點(diǎn)![]() ,當(dāng)線段
,當(dāng)線段![]() 的長等于5時,求直線
的長等于5時,求直線![]() 方程.
方程.
(3)若![]() ,證明直線
,證明直線![]() 必過一定點(diǎn),并求出該定點(diǎn).
必過一定點(diǎn),并求出該定點(diǎn).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)證明見解析,
;(3)證明見解析,![]() .
.
【解析】
試題分析:(1)由![]() ,得
,得![]() ,拋物線
,拋物線![]() 的方程為
的方程為![]() ,進(jìn)而求解拋物線的準(zhǔn)線方程;(2)若直線
,進(jìn)而求解拋物線的準(zhǔn)線方程;(2)若直線![]() 經(jīng)過焦點(diǎn)
經(jīng)過焦點(diǎn)![]() ,則直線
,則直線![]() 的方程為
的方程為![]() ,即可求解
,即可求解![]() 和
和![]() ,再由
,再由![]() ,即可求解該直線
,即可求解該直線![]() 方程;(3)設(shè)直線
方程;(3)設(shè)直線![]() 的方程為
的方程為![]() 代入
代入![]() ,得
,得![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,
,![]() ,再利用
,再利用![]() ,求得
,求得![]() ,即可判定直線過定點(diǎn).
,即可判定直線過定點(diǎn).
試題解析:(1)由![]() ,得
,得![]() ,拋物線
,拋物線![]() 的方程為
的方程為![]() ,
,
其準(zhǔn)線方程為![]() ,焦點(diǎn)為
,焦點(diǎn)為![]() .
.
(2)若直線![]() 經(jīng)過拋物線
經(jīng)過拋物線![]() 的焦點(diǎn)
的焦點(diǎn)![]() ,則直線
,則直線![]() 的方程為
的方程為![]() .
.
![]() ,
,![]() ,則
,則![]() ,
,
所以![]() ,得
,得![]() ,
,![]() ,直線
,直線![]() 方程為
方程為![]() .
.
(3)設(shè)直線![]() 的方程為
的方程為![]() 代入
代入![]() ,得
,得![]() .
.
設(shè)![]() ,
,![]() ,
,
則![]() ,
,![]() .
.
![]() ,
,
∴![]() ,直線
,直線![]() 必過一定點(diǎn)
必過一定點(diǎn)![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知圓心坐標(biāo)為![]() 的圓
的圓![]() 與
與![]() 軸及直線
軸及直線![]() 分別相切于
分別相切于![]() 、
、![]() 兩點(diǎn),另一圓
兩點(diǎn),另一圓![]() 與圓
與圓![]() 外切,且與
外切,且與![]() 軸及直線
軸及直線![]() 分別相切于
分別相切于![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
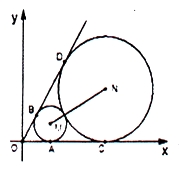
(1)求圓![]() 和圓
和圓![]() 的方程;
的方程;
(2)過點(diǎn)![]() 作直線
作直線![]() 的平行線
的平行線![]() ,求直線
,求直線![]() 被圓
被圓![]() 截得的弦的長度.
截得的弦的長度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】揚(yáng)州瘦西湖隧道長![]() 米,設(shè)汽車通過隧道的速度為
米,設(shè)汽車通過隧道的速度為![]() 米/秒
米/秒![]() .根據(jù)安全和車流的需要,當(dāng)
.根據(jù)安全和車流的需要,當(dāng)![]() 時,相鄰兩車之間的安全距離
時,相鄰兩車之間的安全距離![]() 為
為![]() 米;當(dāng)
米;當(dāng)![]() 時,相鄰兩車之間的安全距離
時,相鄰兩車之間的安全距離![]() 為
為![]() 米(其中
米(其中![]() 是常數(shù)).當(dāng)
是常數(shù)).當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() .
.
(1)求![]() 的值;
的值;
(2)一列由![]() 輛汽車組成的車隊(duì)勻速通過該隧道(第一輛汽車車身長為
輛汽車組成的車隊(duì)勻速通過該隧道(第一輛汽車車身長為![]() 米,其余汽車車身長為
米,其余汽車車身長為![]() 米,每輛汽車速度均相同).記從第一輛汽車車頭進(jìn)入隧道,至第
米,每輛汽車速度均相同).記從第一輛汽車車頭進(jìn)入隧道,至第![]() 輛汽車車尾離開隧道所用的時間為
輛汽車車尾離開隧道所用的時間為![]() 秒.
秒.
①將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
②要使車隊(duì)通過隧道的時間![]() 不超過
不超過![]() 秒,求汽車速度
秒,求汽車速度![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知α、β是不同的平面,l、m、n是不同的直線,P為空間中一點(diǎn).若α∩β=l,mα、nβ、m∩n=P,則點(diǎn)P與直線l的位置關(guān)系用符號表示為___.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期為π.
(Ⅰ)求ω的值;
(Ⅱ)將函數(shù)y=f(x)的圖象上各點(diǎn)的橫坐標(biāo)縮短到原來的![]() ,縱坐標(biāo)不變,得到函數(shù)y=g(x)的圖象,求函數(shù)y=g(x)在區(qū)間
,縱坐標(biāo)不變,得到函數(shù)y=g(x)的圖象,求函數(shù)y=g(x)在區(qū)間![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校某研究性學(xué)習(xí)小組在對學(xué)生上課注意力集中情況的調(diào)查研究中,發(fā)現(xiàn)其在40分鐘的一節(jié)課中,注意力指數(shù)![]() 與聽課時間
與聽課時間![]() (單位:分鐘)之間的關(guān)系滿足如圖所示的圖象,當(dāng)
(單位:分鐘)之間的關(guān)系滿足如圖所示的圖象,當(dāng)![]() 時,圖象是二次函數(shù)圖象的一部分,其中頂點(diǎn)
時,圖象是二次函數(shù)圖象的一部分,其中頂點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() ;當(dāng)
;當(dāng)![]() 時,圖象是線段
時,圖象是線段![]() ,其中
,其中![]() .根據(jù)專家研究,當(dāng)注意力指數(shù)大于62時,學(xué)習(xí)效果最佳.
.根據(jù)專家研究,當(dāng)注意力指數(shù)大于62時,學(xué)習(xí)效果最佳.

(1)試求![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)教師在什么時段內(nèi)安排內(nèi)核心內(nèi)容,能使得學(xué)生學(xué)習(xí)效果最佳?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)已知![]() ,求
,求![]() 單調(diào)遞增區(qū)間;
單調(diào)遞增區(qū)間;
(2)是否存在實(shí)數(shù)![]() ,使
,使![]() 的最小值為0?若存在,求出
的最小值為0?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 的三個頂點(diǎn)
的三個頂點(diǎn)![]() ,
,![]() ,
,![]() ,其外接圓為
,其外接圓為![]() .
.
(1)求![]() 的面積;
的面積;
(2)若直線![]() 過點(diǎn)
過點(diǎn)![]() ,且被
,且被![]() 截得的弦長為2,求直線
截得的弦長為2,求直線![]() 的方程;
的方程;
(3)對于線段![]() 上的任意一點(diǎn)
上的任意一點(diǎn)![]() ,若在以
,若在以![]() 為圓心的圓上都存在不同的兩點(diǎn)
為圓心的圓上都存在不同的兩點(diǎn)![]() ,
,![]() ,使得點(diǎn)
,使得點(diǎn)![]() 的線段
的線段![]() 的中點(diǎn),求
的中點(diǎn),求![]() 的半徑
的半徑![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com