
【題目】選修4—1:幾何證明選講
如圖,已知AP是⊙O的切線,P為切點,AC是⊙O的割線,與⊙O交于B、C兩點,圓心O在∠PAC的內部,點M是BC的中點.

(1) 證明:A、P、O、M四點共圓;
(2)求∠OAM+∠APM的大小
【答案】(1)詳見解析 (2) 90°
【解析】
試題分析:(1)證明四點共圓,一般利用對角互補進行證明:根據相切及垂徑定理得OP⊥AP及OM⊥BC,從而得∠OPA+∠OMA=180°. (2)根據四點共圓得同弦所對角相等:∠OAM=∠OPM,因此
∠OPM+∠APM=90°,
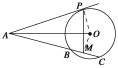
試題解析:(1)證明 連接OP,OM,因為AP與⊙O相切于點P,所以OP⊥AP.
因為M是⊙O的弦BC的中點,所以OM⊥BC,
于是∠OPA+∠OMA=180°.
由圓心O在∠PAC的內部,可知四邊形APOM的對角互補,所以A、P、O、M四點共圓.
(2)解 由(1)得A、P、O、M四點共圓,
所以∠OAM=∠OPM,
由(1)得OP⊥AP,因為圓心O在∠PAC的內部,
所以∠OPM+∠APM=90°,
所以∠OAM+∠APM=90°.


科目:高中數學 來源: 題型:
【題目】中國象棋中規定:馬走“日”字,象走“田”字.如下圖,在中國象棋的半個棋盤(![]() 的矩形中每個小方格都是單位正方形)中,若馬在
的矩形中每個小方格都是單位正方形)中,若馬在![]() 處,可跳到
處,可跳到![]() 處,也可跳到
處,也可跳到![]() 處,用向量
處,用向量![]() ,
,![]() 表示馬走了“一步”.通過探究,你能在圖中畫出馬在
表示馬走了“一步”.通過探究,你能在圖中畫出馬在![]() 處走了一步的所有情況嗎?
處走了一步的所有情況嗎?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—5:不等式選講
已知函數f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集為{x|-2≤x≤3},求實數a的值;
(2)在(1)的條件下,若存在實數n使f(n)≤m-f(-n)成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某地區某高傳染性病毒流行期間,為了建立指標顯示疫情已受控制,以便向該地區居民顯示可以過正常生活,有公共衛生專家建議的指標是“連續7天每天新增感染人數不超過5人”,根據連續7天的新增病例數計算,下列各個選項中,一定符合上述指標的是__________.
①平均數![]() ; ②標準差
; ②標準差![]() ; ③平均數且標準差
; ③平均數且標準差![]() ;
;
④平均數![]() 且極差小于或等于2; ⑤眾數等于1且極差小于或等于4.
且極差小于或等于2; ⑤眾數等于1且極差小于或等于4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學高一學生的數學與地理的水平測試成績抽樣統計如下表:若抽取的學生數為![]() ,成績分為
,成績分為![]() (優秀)、
(優秀)、![]() (良好)、
(良好)、![]() (及格)三個等級,設
(及格)三個等級,設![]() ,
, ![]() 分別表示數學成績與地理成績.例如:表中地理成績為
分別表示數學成績與地理成績.例如:表中地理成績為![]() 等級的共有
等級的共有![]() 人,數學成績為
人,數學成績為![]() 級且地理成績為
級且地理成績為![]() 等級的有8人.已知
等級的有8人.已知![]() 與
與![]() 均為
均為![]() 等級的頻率是0.07.
等級的頻率是0.07.
(1)設在該樣本中,數學成績優秀率是![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)已知![]() ,
, ![]() ,求數學成績為
,求數學成績為![]() 等級的人數比數學成績為
等級的人數比數學成績為![]() 等級的人數多的概率.
等級的人數多的概率.
人數
|
|
|
|
| 14 | 40 | 10 |
|
| 36 |
|
| 28 | 8 | 34 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網店經營的一種商品進行進價是每件10元,根據一周的銷售數據得出周銷售量![]() (件)與單價
(件)與單價![]() (元)之間的關系如下圖所示,該網店與這種商品有關的周開支均為25元.
(元)之間的關系如下圖所示,該網店與這種商品有關的周開支均為25元.

(1)根據周銷售量圖寫出![]() (件)與單價
(件)與單價![]() (元)之間的函數關系式;
(元)之間的函數關系式;
(2)寫出利潤![]() (元)與單價
(元)與單價![]() (元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.
(元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列問題中符合調查問卷要求的是( )
A.你們單位有幾個高個子?
B.您對我們廠生產的電視機滿意嗎?
C.您的體重是多少千克?
D.很多顧客都認為該產品的質量很好,您不這么認為嗎?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-1《幾何證明選講》
已知A、B、C、D為圓O上的四點,直線DE為圓O的切線,AC∥DE,AC與BD相交于H點

(1)求證:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com